总结
- 本文主要是通过数学的方法分析现有GAN训练中存在的问题
- 先从KL散度入手——散度不对称对于两种不同的损失(真实分布存在而生成分布不存在;真实分布不存在而生成分布存在)给予了两种截然不同的惩罚
- 然后分析了训练过程不稳定的原因
- 当生成器的损失函数是$E_{x \sim P_r}[logD(x)] + E_{x \sim P_g}[log(1 - D(x))]$=$ 2JS(P_r||P_g) - 2log2$时,在分类器最优时,此损失函数是一个常数(低维流形理论JS散度一直为常数$log2$),根本没有梯度,所以随着存在梯度消失的问题
- 当生成器的损失函数是$-logD$ = $KL(P_g||P_r) - 2JS(P_r||P_g)$时有两个问题。第一个是两个散度的优化方向矛盾,一个是让两个分布尽量近一个是尽量远,导致训练方向不稳定;另外KL的散度加大了对于$P_r = 0 且 P_g = 1$的惩罚,导致模型坍塌
- 提出解决方案——给两个分布加噪音,使两个低维流形维度升高,产生重叠,从而使JS散度不为常数,之后慢慢将噪声去除
- 提出Wasserstein距离,但是没有过多讨论,留到下一篇Wasserstein GAN再说
Abstract
this paper is proposed to make theoretical steps towards fully understanding the training dynamics of GANs
three sections:
- the problem at hand
- studying and proving rigorously the problems including instability and saturation
- examines a practical and theoretically grounded direction towards solving these problems
Introduction
this paper aims to change unstable behaviour of GANs by providing a solid understanding of these issues, and create principled research direction towards adressing them
KL divergence
traditional approaches is to minimize:
this divergence is not symmetrical between $P_r$ and $P_g$:
- if $P_r(x) > P_g(x)$ that means generator can not generate real data. KL grows quickly to infinity
- if $P_r(x) < p_g(x)$ that means generator output a image that doesn’t look real. KL goes to 0
if we would minimize $KL(P_g||P_r)$ instead, meaning that this cost function would pay a high cost for generating not plausibly looking pictures
optimization gets massively unstable
several questions:
- Why do updates get worse as the discriminator gets better? Both in the original and the new cost function.
- Why is GAN training massively unstable?
- Is the new cost function following a similar divergence to the JSD? If so, what are its
properties? - Is there a way to avoid some of these issues?
The fundamental contributions of this paper are the answer to all these questions
Source of instability
the discriminator will have cost at most $2log2 - 2JSD(P_r||P_g)$, in practice, if we just train D till convergence, its error will go to 0
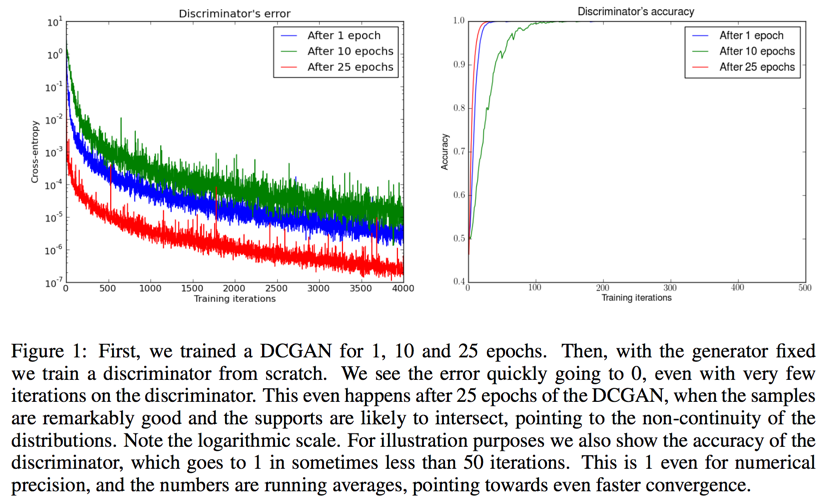
if the supports of $P_r$ and $P_g$ are disjoint or lie in low dimensional manifolds, there is always a perfect discriminator between them
the perfect discriminator theorems
- we will first explain the case where $P_r$ and $P_g$ have disjoint supports
Theorem 2.1:
- in the next theorem, we take away the disjoint assumption
we can safely assume in practice that any two manifolds never perfectly align


- We now state our perfect discrimination result for the case of two manifolds


if these divergencies are always maxed out attempting to minimize them by gradient descent isn’t really possible
the consequences, and the problems of each cost function
If the two distributions we care about have supports that are disjoint or lie on low dimensional manifolds, the optimal discriminator will be perfect and its gradient will be zero almost everywhere
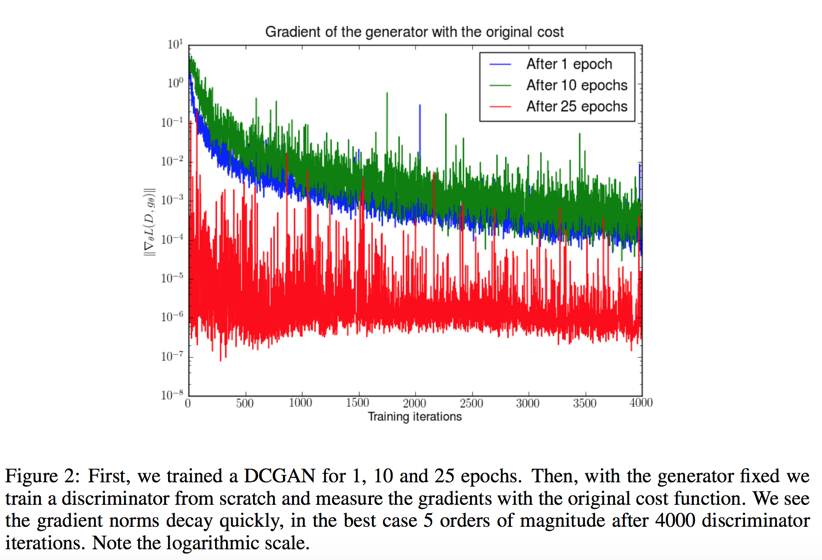
the original cost function

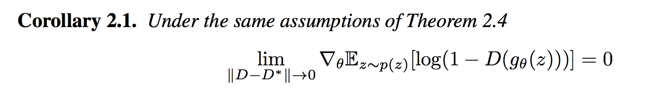
This shows that as our discriminator gets better, the gradient of the generator vanishes
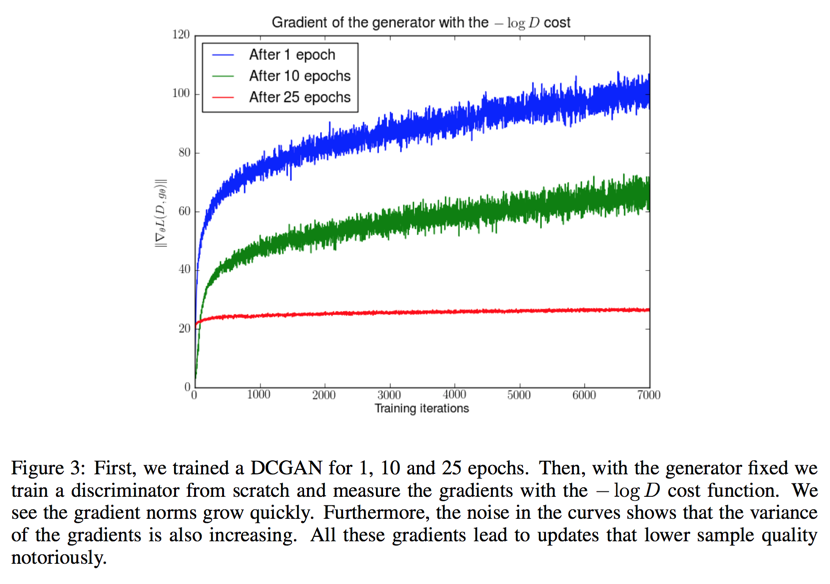
the $-logD$ alternative
the avoid gradients vanishing, people use another gradient step:
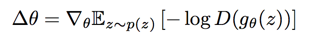
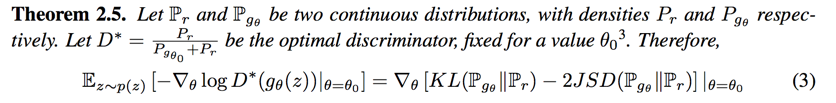

Towards Softer Metrics and Distributions
An important question now is how to fix the instability and vanishing gradients issues
Something we can do to break the assumptions of these theorems is add continuous noise to the inputs of the discriminator
skip the looooooots of proof……