时间序列总结

自回归模型（AR）

概述

• 自回归模型一种时间序列预测模型，是若干随机数的集合。描述的是当前值与历史值得关系，是一种随机过程
• 对于指定值的预测是对于以往值的线性预测加上随机扰动项，所以这个模型的形式是一个随机差分方程
• 是ARMA（Autoregressive–moving-average model）和VAR（Vector Autoregressive model）一种特殊形式
• p阶自回归模型记作AR(p)

定义

AR(p)模型的定义如下

$$X_t = c + \sum_{i = 1}^{p} \varphi_i X_{t-i} + \varepsilon_t$$

其中$ \varphi_i … \varphi_p $是模型的参数，c是常数，$\varepsilon_t$是白噪声随机数
其中$\varepsilon_t$ 服从平均值为0 方差为$\sigma^2$ 的的正态分布，即$\varepsilon_t \sim N(0, \sigma)$
引入滞后算子B将公式变形如下

$$X_t = c + \sum_{i = 1}^{p} \varphi_iB^iX_t + \varepsilon_t$$

将求和公式部分移到左边

$$(1 - \sum_{i = 1}^{p} \varphi_iB^i)X_t = c + \varepsilon_t$$

左侧$X_t$的系数是一个多项式，简化表示为

$$\phi(B)X_t = c + \varepsilon_t$$

至此AR(p)模型可以看做为一个输入为白噪声的滤波器

序列平稳

由于我们建立模型的目的主要是预测未来走势，然后才是更好的理解数据，这就要求随机变量的基本特性具有可延续性

平稳的时间序列：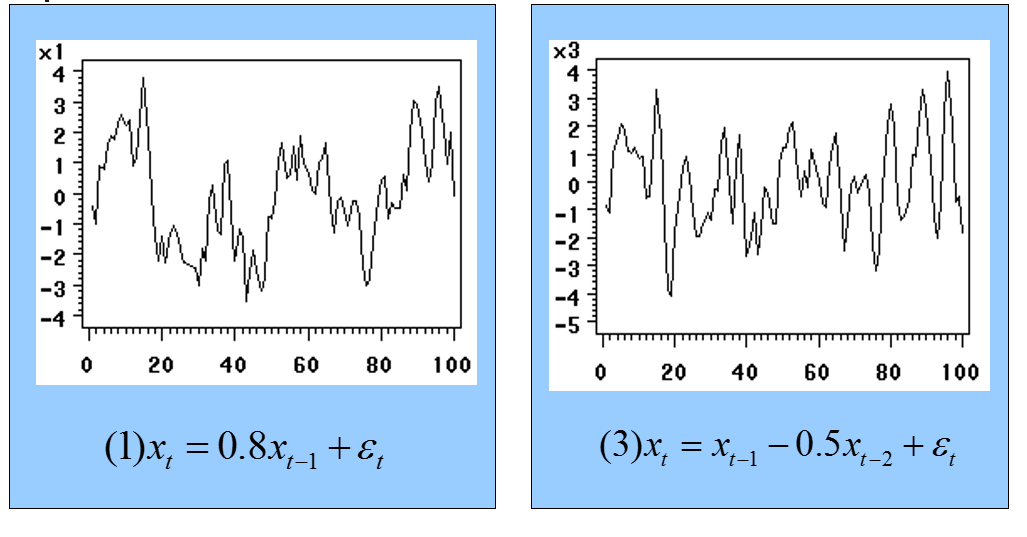

非平稳的时间序列：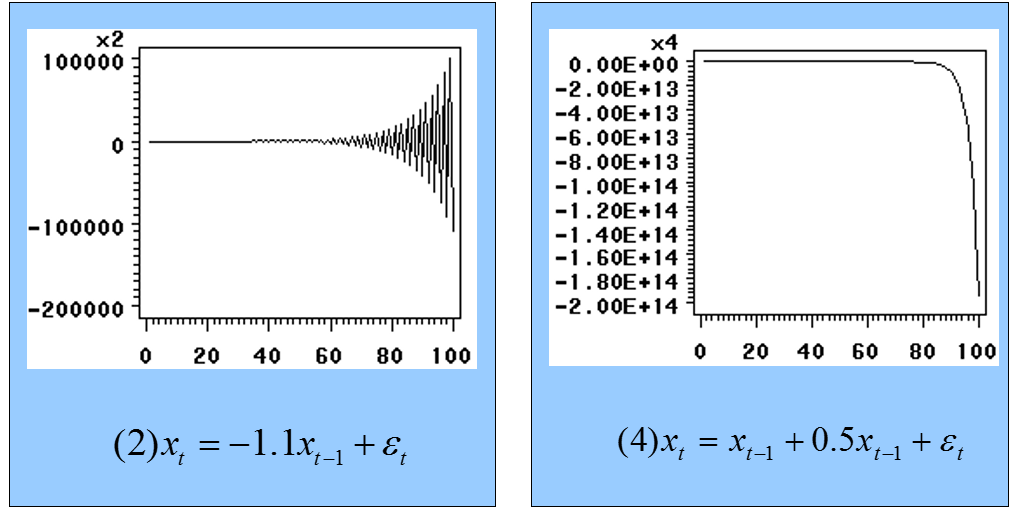

是否平稳的考量范围：

• 均值与统计时间无关
• 方差与统计时间无关
• 协方差与统计时间无关，只与统计间隔有关

满足上述所有条件的话序列称为广义平稳

AR(p)模型平稳的充要条件是回归系数多项式$\phi(B)$的根都在单位圆外

适用范围

仅通过时间序列变量的自身历史观测值来反映有关因素对预测目标的影响和作用，不受模型变量相互独立的假设条件约束，所构成的模型可以消除普通回归预测方法中由自变量选择、多重共线性等造成的困难

模型判定

判断一组数据属于哪个时间序列模型，主要取决于数据的自相关函数和偏自相关函数 ，下面介绍一下这几个概念

自相关系数/协方差

用于衡量两个变量的总体误差
期望值分别为$E(X) = \mu$和$E(Y) = \nu$的协方差定义为

$$cov(X, Y) = E((X- \mu)(Y - \nu))$$ $$cov(X, Y) = E(X \cdot Y) - \mu\nu$$

时间序列中的协方差简写为$\gamma_i$代表$cov(X_t, X_{t-i})$
其中$\gamma_0$就代表了变量的方差$var(X_t)$

自相关函数

又名序列相关函数，表明距离为$i$的两个数据点的相关性
定义为：

$$\rho_i = \frac {\gamma_i} {var(Xt)} 即 \rho_i = \frac {\gamma_i} {\gamma_0}$$

偏自相关函数

就是在原自相关函数的基础上，给定中间的变量的情况下$X_t$与$X_{t - i}$的相关度度量，定义为

$$\phi_i = \rho_{X_t, X_{t - i} | X_{t-1}, \cdots , X_{t - i + 1}}$$

根据定义可知，其实AR模型中的$\phi_i$的值就是模型的第i个参数的值

模型特点

首先求解(序列均值为0的)$AR(p)$的自相关系数，原式两边同乘以$X_{t - k}$

$$X_{t - k}X_t = \phi_1X_{t - k}X_{t - 1} + \phi_2X_{t - k}X_{t - 2} + \dots + \phi_pX_{t - k}X_{t - p}$$

两边同时取期望

$$E[X_{t - k}X_t] = \phi_1E[X_{t - k}X_{t - 1}] + \phi_2E[X_{t - k}X_{t - 2}] + \dots + \phi_pE[X_{t - k}X_{t - p}]$$

由于序列均值为0所以

$$cov(X_t, X_{t - k} ) = E[(X_t - 0)(X_{t - k} - 0)] \\ = E[X_t \cdot X_{t - k}]$$

即序列中不同时刻的两个变量的协方差就是他们乘积的期望
所以$AR(p)$自相关系数为：

$$\gamma_k = \phi_1\gamma_{k - 1} + \phi_2\gamma_{k - 2} + \dots + \phi_p\gamma_{k - p}$$

以$X_t = 0.8X_{t - 1} + \varepsilon_t$为例

1. 自相关函数拖尾——指数级递减，衰减至0
   
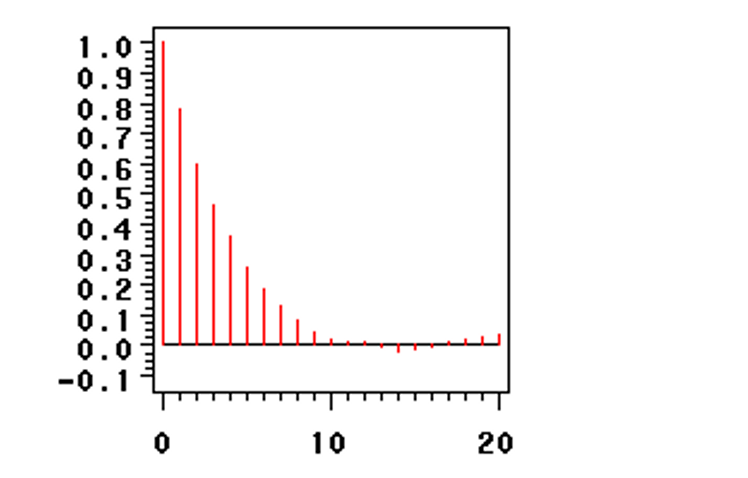
2. 偏自相关函数P阶截尾
   

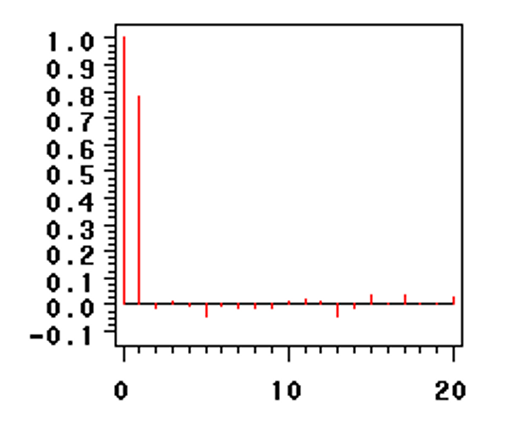
模型参数求解

模型参数的求解方式有多种，例如最小二乘法、矩估计、Yule-Walker估计、最大似然估计

最小二乘法

计算简单，不需要计算偏自相关函数

Yule-Walker估计

在AR模型中，参数和模型的协方差函数存在着某种联系，而两者存在的关系也可以从自相关函数中直接求解模型参数。Yule-Walker 方程清晰的展现了两者的关系。对于一个p阶AR模型AR(p)，方程形式如下

$$\gamma_m = \sum_{k = 1}^p\varphi_k\gamma_{m-k} + \sigma_{\varepsilon}^2\delta_{m,0}$$

其中$\gamma_m$是$X_t$的的自协方差，$\sigma_{\varepsilon}^2$是白噪声的方差，$\delta_{m,0}$是克罗内克符号
穷举$m = 0,\ldots,p$可以得到p + 1 个方程，由于第一个方程有些特殊（多了一个常数项），我们把他单独拿出来处理，剩下的方程整理为如下形式

\begin{equation}
\begin{bmatrix}
\gamma_1 \\
\gamma_2 \\
\vdots \\
\gamma_p
\end{bmatrix}
=
\begin{bmatrix}
\gamma_0 & \gamma_{-1} & \gamma_{-2} & \cdots \\
\gamma_1 & \gamma_{0} & \gamma_{-2} & \cdots \\
\vdots & \vdots & \vdots & \ddots \\
\gamma_{p-1} & \gamma_{p-2} & \gamma_{p-3} & \cdots \\
\end{bmatrix}
\begin{bmatrix}
\varphi_1 \\
\varphi_2 \\
\vdots \\
\varphi_p
\end{bmatrix}
\nonumber
\end{equation}

根据上面的等式，当模型的自协方差已知时可以根据上面p个方程求解全部模型参数
然后根据第一个方程$\gamma_0 = \sum_{k=1}^{p}\varphi_k\gamma_{-k} + \sigma_{\varepsilon}^2$计算出$\sigma_{\varepsilon}^2$整个模型的参数就确定下来了

计算相对简单，在小样本情况下表现比最小二乘好，大样本两个方法差不多

最大似然估计

计算复杂，精度高

滑动平均模型（MA）

概述

• 滑动平均模型描述的是自回归过程的误差累计
• q阶滑动平均模型记作MA(q)

定义

MA(q)模型的定义如下

$$X_t = \mu + \varepsilon_t - \theta_1\varepsilon_{t-1} - \dots - \theta_q\varepsilon_{t-q}$$

其中$\mu$代表的是序列均值，$\theta_1 \dots \theta_q$ 是模型的参数值，$\varepsilon_t \dots \varepsilon_{t-q}$是噪音项，他们都服从标准正态分布并且相互独立
引入滞后因子

$$X_{t} = \mu + (1 - \theta_1B - \dots - \theta_qB^q )\varepsilon_t$$

多项式简化表示

$$X_{t} = \mu + \theta(B)\varepsilon_t$$

与自回归模型的白噪声对比

1. 影响方式不同。前几项白噪声直接影响后面的值，而AR模型中前几项的白噪声并没有直接出现在等式右边，只是通过影响前几项的值，然后前几项的值再去间接影响后面的值。
2. 影响范围不同。MA模型的噪声值只能影响当时时刻的值和之后的q个时刻的值，而AR模型的每一项噪声都能对无穷远项产生影响。

转化为AR模型

方程也可写成

$$\theta(B)^{-1}X_t = \varepsilon_t \\ \frac {X_t} {1 - \sum_{i = 1}^q\theta_iB^i} = \varepsilon_t$$

左式泰勒展开的条件是

$$\sum_{i = 1}^q\theta_iB^i < 1 \\ 1 - \sum_{i = 1}^q\theta_iB^i > 0 \\ \phi(B) > 0$$

泰勒展开后

$$(1 + \sum_{i = 1}^q\theta_iB^i + (\sum_{i = 1}^q\theta_iB^i)^2 + \dots)X_t = \varepsilon_t$$

变为无穷多阶AR模型

模型判定

$MA(q)$的自相关系数为

$$\gamma_k = E[(\varepsilon_t - \theta_1\varepsilon_{t - 1} - \dots - \theta_q\varepsilon_{t - q})(\varepsilon_{t - k} - \theta_1\varepsilon_{t - k - 1} - \dots - \theta_q\varepsilon_{t - k - q})] =$$

\begin{cases}
(-\theta_k + \theta_1\theta_{k + 1} + \theta_2\theta_{k + 2} + \dots + \theta_{q - k}\theta_{q})\sigma^2 & k = 1, 2, \dots, q \\
0 & k > q
\end{cases}
以$X_t = \varepsilon_t - 2\varepsilon_{t - 1}$为例

1. 自相关函数q阶截尾
   
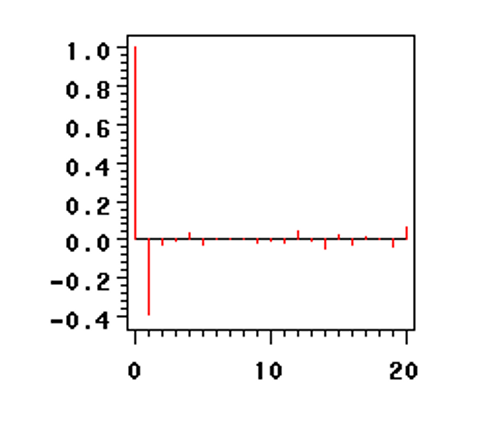
2. 偏自相关函数拖尾
   

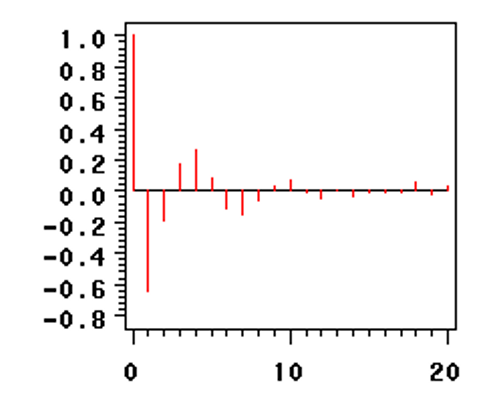
模型参数求解

因为噪声项不可测量的性质，MA模型的求解比AR模型的求解复杂一些，使用曲线拟合或矩估计。

自回归滑动平均模型（ARMA）

概述

• 由自回归模型和滑动平均模型两部分组合而成
• 用于理解甚至预测一组时间序列数据
• p阶自回归模型和q阶滑动回归模型所组合起来的自回归滑动平均模型记作ARMA(p,q)

定义

ARMA(p, q)的定义如下

$$X_t = c + \varepsilon_t + \sum_{i = 1}^p\varphi_tX_{t-i} + \sum_{i = 1}^q\theta_i\varepsilon_{t-i}$$

由自回归模型和滑动平均模型组合而成
引入滞后因子

$$(1 - \sum_{i = 1}^{p} \varphi_iB^i)X_t = (1 - \sum_{i=1}^q\theta B^i )\varepsilon_t$$

化简

$$\varphi(B)X_t = \theta(B)\varepsilon_t$$

或者写成

$$\frac {\varphi(B)} {\theta(B)} X_t = \varepsilon_t$$

模型参数求解

ARMA(p, q)模型无法通过最小二乘法直接解出，通常的做法是先通过数据选择出最小的p和q
一般情况下使用赤池信息量准则去求解p和q

$$AIC(p, q) = ln(\sigma_r^2(p, q)) + \frac {2(p + q)} {N}$$

其中$N$是样本数，$\sigma_r^2$是残差项的方差
选取合适的$p, q$使得AIC最小
得到p和q之后，用高阶AR模型去近似ARMA模型，再通过Yule-Walker方程求解各个参数

模型判定

以$X_t - 0.5X_{t - 1} = \varepsilon_t - 0.8 \varepsilon_{t -1}$为例

1. 自相关函数拖尾
   

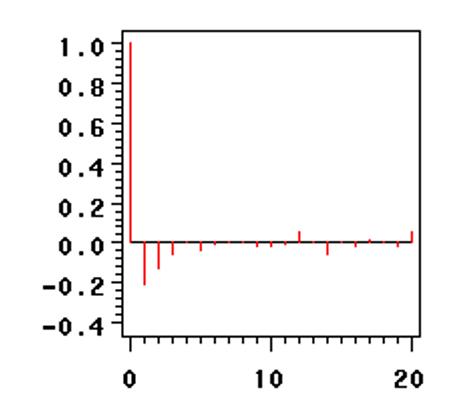
2. 偏自相关函数拖尾
   

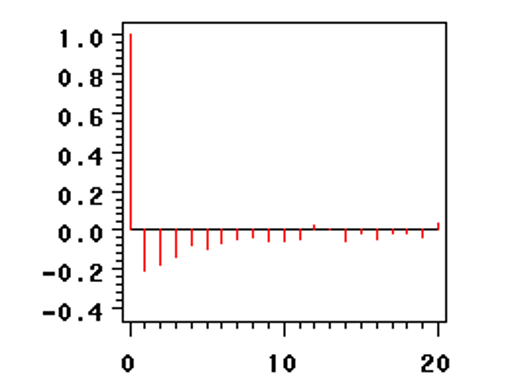
自回归求和滑动平均模型（ARIMA）

概述

• ARIMA全称Autoregressive Integrated Moving Average
• 是ARMA模型的泛化形式
• 适用于数据不平稳的情形
• 通过差分的方式降低数据的不平稳特性然后转化为ARMA模型
• 又称Box-Jenkins法

定义

ARIMA(p, d, q)的定义如下

$$(1- \sum_{i = 1}^p{\varphi_iB^i})(1 - B)^dX_t = (1 - \sum_{i = 1}^q{\theta_iL^i})\varepsilon_t$$

其中$p$是$AR(p)$模型的阶数，$d$是序列成为平稳序列所做的差分次数（阶数），$q$是$MA(q)$模型的阶数

使用平稳序列$W_t = \Delta^d X_t$代替之前的非平稳序列那么$X_t = \Delta^{-d}W_t$
其中$\Delta^{-1}$是无穷级数因为$\Delta^{-1} = (1 -B)^{-1} \\ = 1 + B + B ^ 2 + \dots$
所以$X_t = \Delta^{-d}W_t$可以看做非平稳的序列是由平稳的ARMA序列累加(积分)d次构成，因此成为自回归求和滑动平均模型

模型参数求解

p, d, q中最先确定d，即使序列平稳的差分次数，通常情况下d<3
确定好d之后模型转化为ARMA(p, q)求解

各模型比较

模型	自相关函数	偏相关函数	数据平稳
AR	拖尾	截尾	平稳
MA	截尾	拖尾	平稳
ARMA	拖尾	拖尾	平稳
ARIMA	拖尾	拖尾	不平稳

应用步骤

st=>start
e=>end

cond1=>condition: 时间序列是否平稳
cond2=>condition: 参数显著性检验
cond3=>condition: 模型残差白噪声检验
op1=>operation: 计算样本的自相关函数，偏相关函数
op2=>operation: 通过差分方式平稳序列
op3=>operation: 模型识别
op4=>operation: 模型定阶&参数估计
op6=>operation: 序列预测

st->cond1
cond1(yes)->cond3
cond3(yes)->op6
cond3(no)->op3
cond1(no)->op2
op2->cond3
op1->op3->op4(left)->cond3
op6->e

模型平稳化处理

可通过散点图直观判断——如果序列有明显趋势，那么不平稳
也可通过自相关函数判断——如果自相关函数衰减缓慢，那么不平稳
方差检验——Fisher检验法

如果数据不平稳，那么通过差分的方式将其转化为平稳序列

白噪声检验

如果$X_t$满足:

1. 任取$t \in T$有$EX_t = \mu$
2. 任取$t , s \in T$有

\begin{equation}
cov(t, s) =
\begin{cases}
\sigma^2 & t = s \\
0 & t \neq s
\end{cases}
\end{equation}

那么就称$X_t$为白噪声序列
如果模型的残差是一个白噪声序列，那么说明所有的依赖关系都已经被模型提取，达到了建模的目的

模型识别

计算序列的自相关函数和偏自相关函数，根绝两者的拖尾和截断情况来判断适应的模型
实际：因为由于样本的随机性，样本的相关系数不会呈现出理论截尾的完美情况，本应截尾的或仍会呈现出小值振荡的情况
95%置信区间：如果样本(偏)自相关系数在最初的d阶明显大于两倍标准差范围，而后几乎95％的自相关系数都落在2倍标准差的范围以内，而且通常由非零自相关系数衰减为小值波动的过程非常突然。这时，通常视为(偏)自相关系数截尾。截尾阶数为d

模型定阶

• 对于简单的ARMA模型通过观察自相关函数和偏相关函数可以进行初步定阶
• 复杂的ARMA模型通过赤池信息量准则定阶

模型参数估计

差分之后用ARMA那一套
计算出参数后对于对于不显著为0的项将其去掉，降阶，重新建模

模型预测

得到模型依次求解即可

引用

1. https://www.wikipedia.org/
2. 《时间序列分析简明教程》——张树京，齐立心
3. http://www3.resset.cn:8080/fincm/sas/show.action;jsessionid=4CAC176D4EFABFB5420504B14C86426C?sid=5317bb064b77f967014c314ccb5a000a