A Comprehensive Survey on Graph Neural Networks
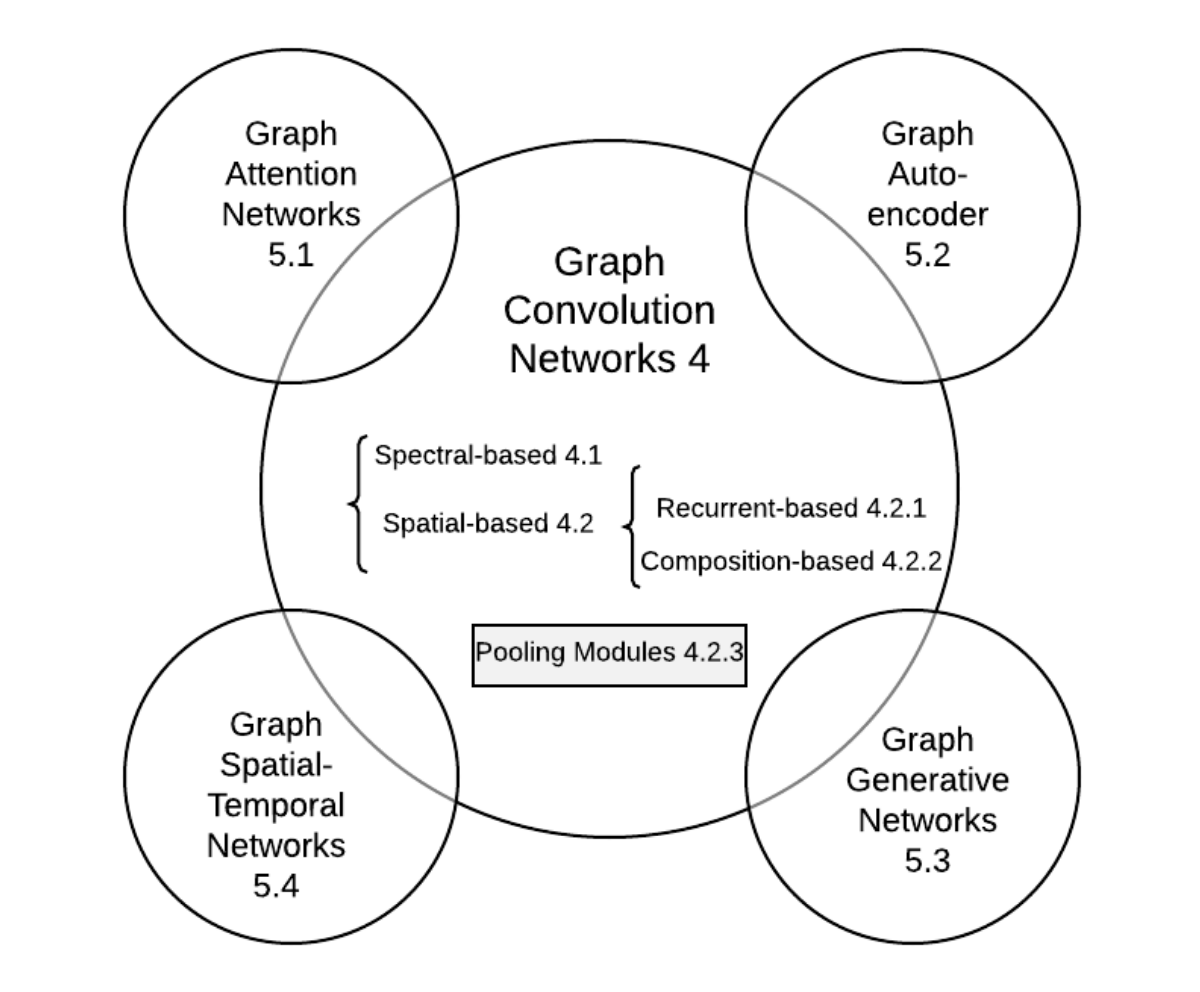
- GNN分类(按更新方式)
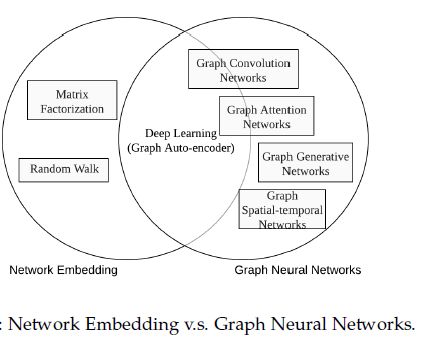
- 与图嵌入的关系
Revisiting Semi-Supervised Learning with Graph Embeddings
Related Work
Graph-Based Semi-Supervised Learning
- Graph-based semi-supervised learning is based on the assumption that nearby nodes tend to have the same labels.
Loss:
- the first term is the standard supervised loss function
- The second term is the graph Laplacian regularization, which incurs a large penalty when similar nodes with a large $w_{ij}$ are predicted to have different labels
Learning Embeddings
A number of embedding learning methods are based on the Skipgram model, which is a variant of the softmax model
Loss:
- $C$ is the set of all possible context
- $w$ are parameters of the Skipgram model
- $e_i$ is the embedding of instance $i$
Application:
- word2vec(NLP)
- Deepwalk(Graph)
- LINE(multiple context spaces)
Semi-Supervised Learning with Graph Embeddings
Loss:
- $\mathcal{L}_s$ is a supervised loss of predicting the labels
- $\mathcal{L}_u$ is an unsupervised loss of predicting the graph context
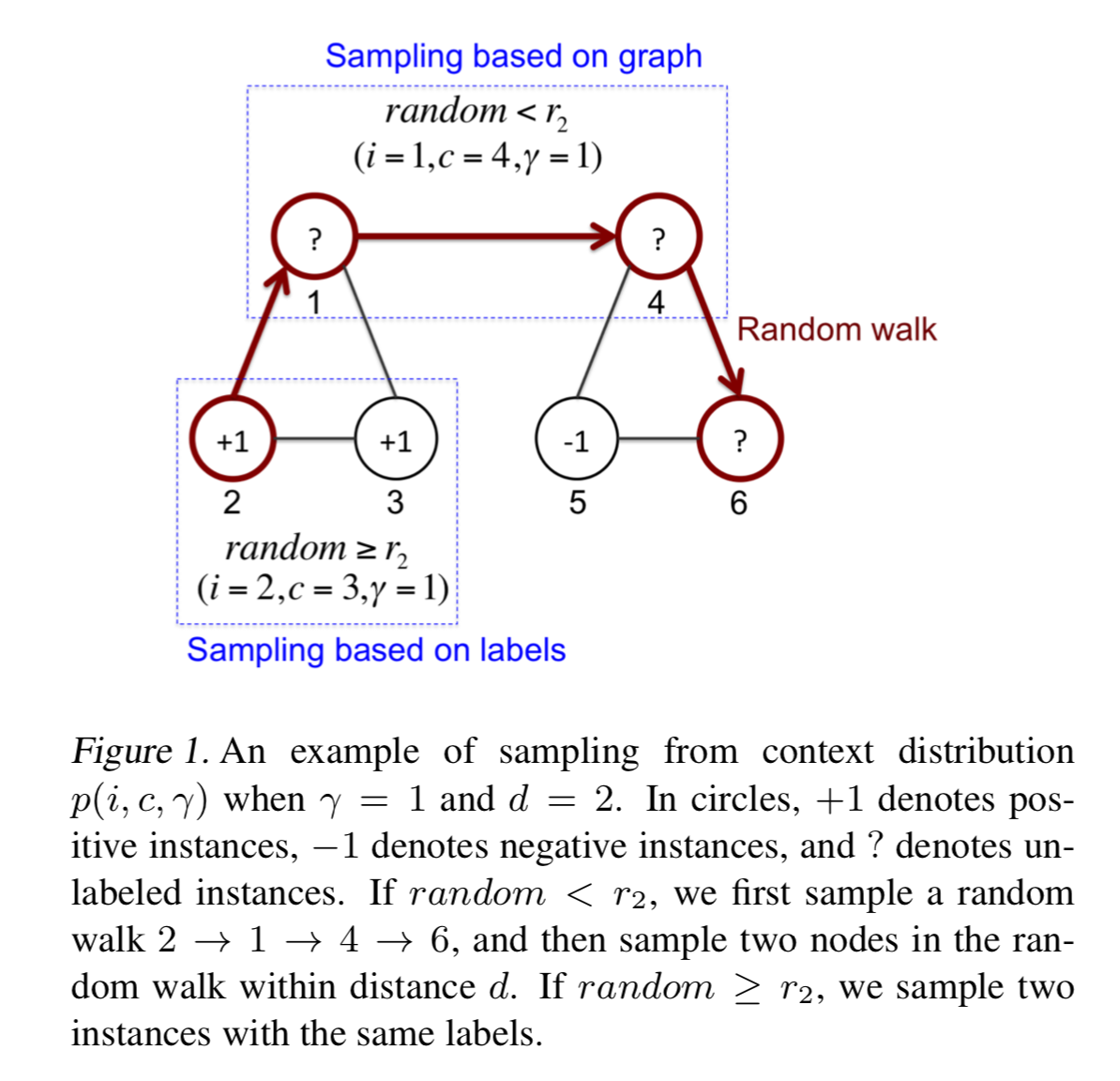
Sampling Context
We formulate the unsupervised loss $\mathcal{L}_u$ as a variant of Skipgram loss
negative sampling:
we are sampling $(i, c, γ)$ from a distribution, where $i$ and $c$ denote instance and context respectively, $γ = +1$ means $(i, c)$ is a positive pair and $γ = −1$ means negative. Given $(i, c, γ)$, we minimize the cross entropy loss of classifying the pair $(i, c)$ to a binary label $γ$:
sampling algorithm:

example:
Transductive Formulation
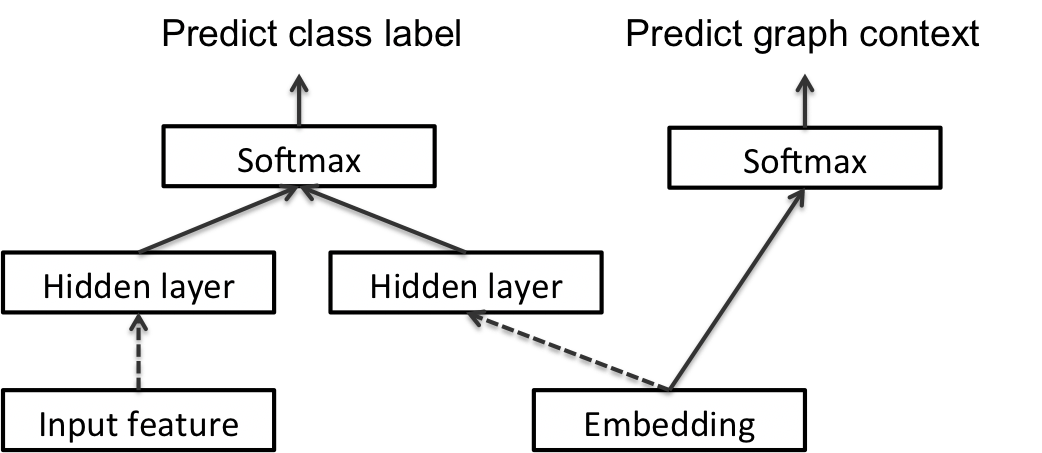
The two hidden layers are concatenated, and fed to a softmax layer to predict the class label of the instance
Inductive Formulation
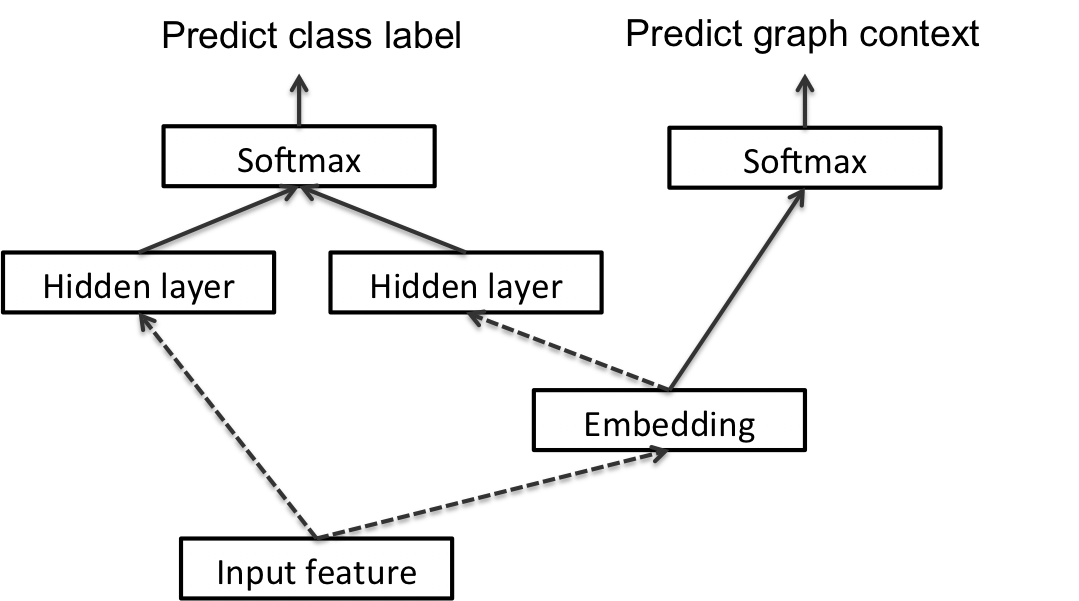
Conclusion
contributions:
- incontrast to previous semi-supervised learning approaches that largely depend on graph Laplacian regularization, we propose a novel approach by joint training of classification and graph context prediction
- since it is difficult to generalize graph embeddings to novel instances, we design a novel inductive approach that conditions embeddings on input features
ANRL: Attributed Network Representation Learning via Deep Neural Networks
issues:
- network topology and node attributes are two heterogeneous information sources, thus it is challenging to preserve their properties in a common vector space
- the observed network data is often incomplete and even noisy, which brings more difficulties for obtaining informative representations
contributions:
- integrates network structural proximity and node attributes affinity into low-dimensional representation spaces
- we design a neighbor enhancement autoencoder, which can retain better similarity between data samples in the representation space
- We also propose an attribute-aware skip-gram model to capture the structure correlations
- These two components share connections to the encoder
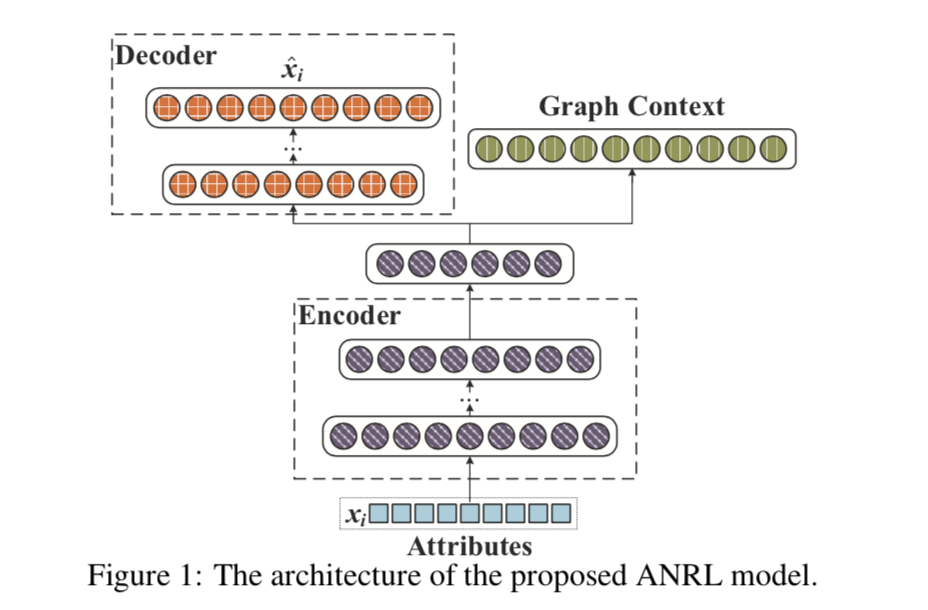
Proposed Model
problem formulation
we aim to represent:
- each node $i ∈ V$ as a low-dimensional vector $y_i$
- mapping function f preserves not only network structure but also node attribute proximity
neighbor enhancement autoencoder
Loss:
- $\hat{x}_i$ is the reconstruction output of decoder
- $T(v_i)$ returns the target neighbors of $v_i$
- $T(·)$ incorporates prior knowledge into the model and can be adopted by the following two formulations:
- Weighted Average Neighbor
- Elementwise Median Neighbor
attribute-aware skip-gram model
Loss:
where:
- $v_{i+j}$ is the node context in the generated random sequence
- $b$ is the window size
negative sampling:
for a specific node-context pair $(v_i,v_{i+j})$, we have the following objective:
where:
- $P_n(v) ∝ d_v^{3/4}$ as suggested in [Mikolov et al., 2013b]
- where $d_v$ is the degree of node v
joint optimization
Loss:
Conclusions
- incorporates both node attributes and network structure information into the embedding
- To further address the structure proximity and attribute affinity preserving, we develop a neighbor enhancement autoencoder and attribute-aware skip-gram model to exploit the complex interrelations between structural information and attributes
DeepWalk: Online Learning of Social Representations
the sparsity of a network representation is both a strength and a weakness:
- Sparsity enables the design of efficient discrete algorithms
- but can make it harder to generalize in statistical learning
We develop an algorithm (DeepWalk) that learns social representations of a graph’s vertices, by modeling a stream of short random walks
DeepWalk takes a graph as input and produces a latent representation as an output
We propose an unsupervised method which learns features that capture the graph structure independent of the labels’ distribution.
Learning Social Representations
We seek learning social representations with the following characteristics:
- Adaptability - Real social networks are constantly evolving; new social relations should not require repeating the learning process all over again.
- Community aware - The distance between latent dimensions should represent a metric for evaluating social similarity between the corresponding members of the network. This allows generalization in networks with homophily.
- Low dimensional - When labeled data is scarce, low-dimensional models generalize better, and speed up convergence and inference.
- Continuous - We require latent representations to model partial community membership in continuous space. In addition to providing a nuanced view of community membership, a continuous representation has smooth decision boundaries between communities which allows more robust classification.
random walks
We denote a random walk rooted at vertex $v_i$ as $W_{v_i}$ . It is a stochastic process with random variables $W_{v_i}^1 ,W_{v_i}^2 ,…,W_{v_i}^k$
such that $W_{v_i}^{k + 1}$ is a vertex chosen at random from the neighbors of vertex $v_k$
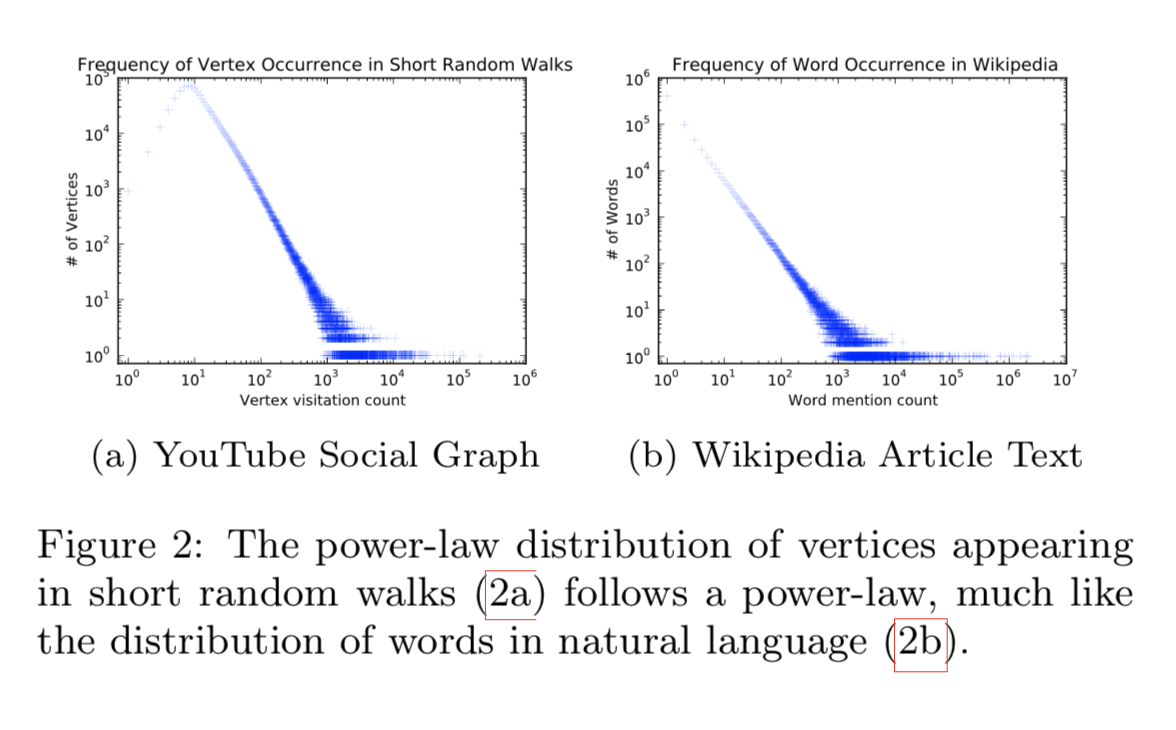
connection: power laws
we observe that the frequency which vertices appear in the short random walks will also follow a power-law distribution
word frequency in natural language follows a similar distribution
Language Modeling
relaxations:
from
to
- First, the order independence assumption better captures a sense of nearness that is provided by random walks.
- Moreover, this relaxation is quite useful for speeding up the training time by building small
models as one vertex is given at a time
Method
DeepWalk
the algorithm consists of two main components:
- a random walk generator
- an update procedure
A walk samples uniformly from the neighbors of the last vertex visited until the maximum $length(t)$ is reached

At the start of each pass we generate a random ordering to traverse the vertices. This is not strictly required, but is well-known to speed up the convergence of stochastic gradient descent.
skipgram
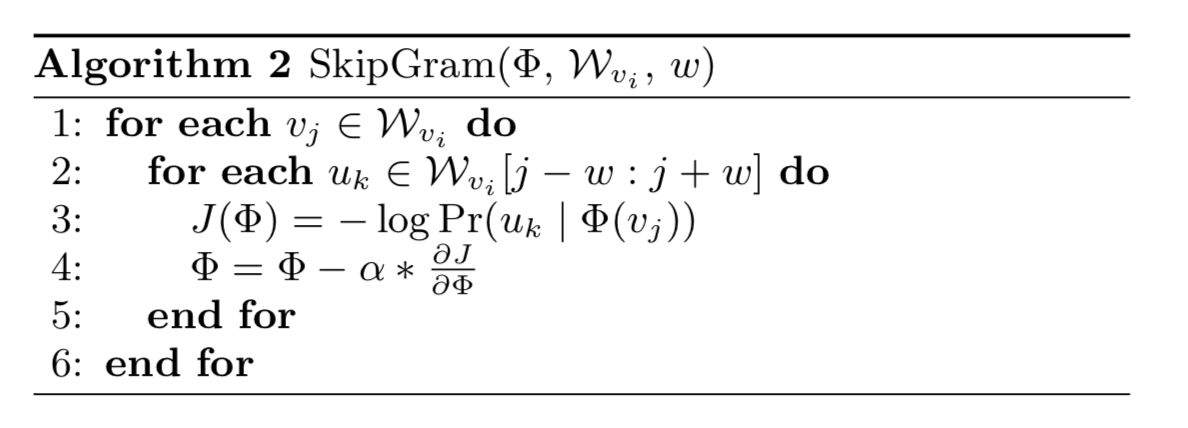
To speed the training time, Hierarchical Softmax can be used to approximate the probability distribution
hierarchical softmax
we assign the vertices to the leaves of a binary tree, the prediction problem turns into maximizing the probability of a specific path in the tree
Huffman coding is used to reduce the access time of frequent elements in the tree
Variants
- Streaming
- Non-random walks
LINE: Large-scale Information Network Embedding
- We propose a novel network embedding model called the “LINE,” which suits arbitrary types of information networks and easily scales to millions of nodes. It has a carefully designed objective function that preserves both the first-order and second-order proximities.
- We propose an edge-sampling algorithm for optimizing the objective. The algorithm tackles the limitation of the classical stochastic gradient decent and improves the effectiveness and efficiency of the inference.
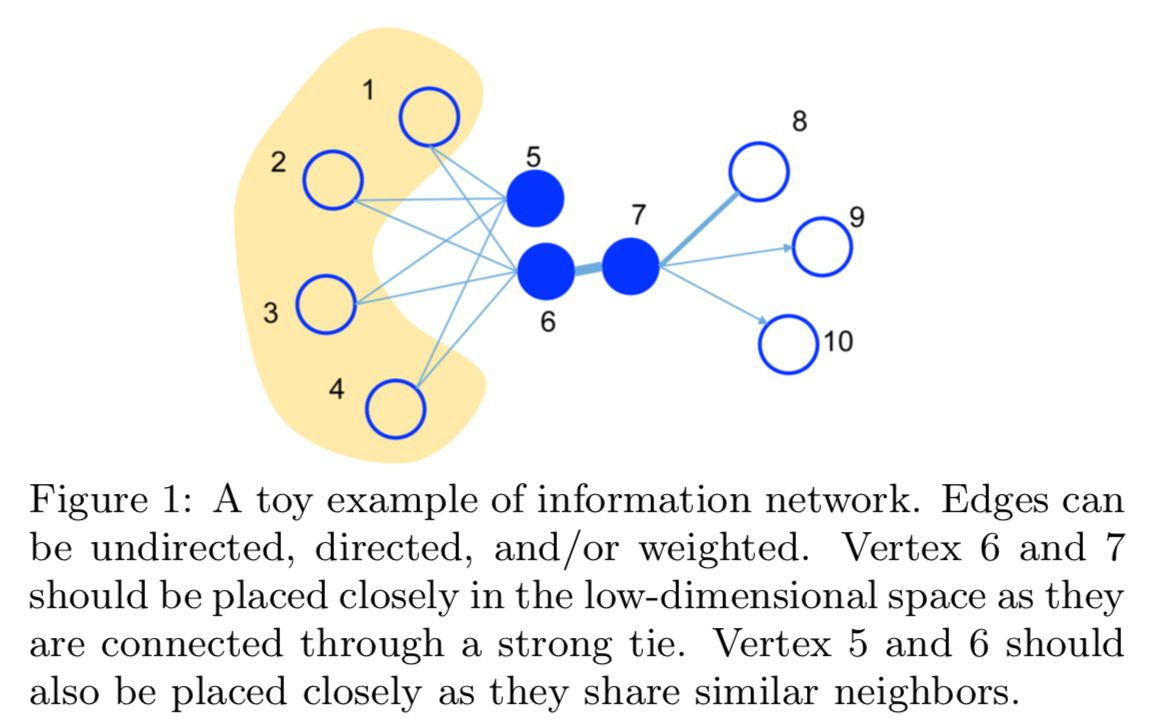
Problem definition
First-order Proximity:
the local pairwise proximity between two vertices
Second-order Proximity:
proximity between a pair of vertices (u,v) in a network is the similarity between their neighborhood network structures
Large-Scale Information Network Embedding
LINE with First-order Proximity
define the joint probability between vertex $v_i$ and $v_j$ as follows:
empirical probability:
objective function:
Replacing d(·, ·) with KL-divergence and omitting some constants, we have:
LINE with Second-order Proximity
define the joint probability between vertex $v_i$ and $v_j$ as follows:
empirical probability:
objective function:
Replacing d(·, ·) with KL-divergence and omitting some constants, we have:
Model Optimization
- negative sampling
- Optimization via Edge Sampling