Non-local Neural Networks

总结

• 本文针对CNN对局部信息的计算提出了一种新的操作结构，用来捕获全局信息之间的关系
• 所谓non-local计算就是当计算某一点的响应结果时，将全局响应值带权求和
• 使用non-local有以下几个好处:
  • 计算某一点的输出时考虑该点与全局的相关性
  • 计算不复杂的同时可以涨点
  • non-local操作保持原输入输出的尺寸不变，可以方便的加到网络中去
• 通用公式：$y_i= \frac {1} {C(x)}\sum_{\forall j}f(x_i, x_j)g(x_j)$
  • 通常g函数就选为1*1卷积
  • f函数一版选择Embedded Gaussian高斯函数，选择其他几种实际效果差距不大
  • 特别说明一点当f函数选择为Embedded Gaussian时，公式就等同于self-attention的形式，说明self-attention是non-local的一种特例
• 在non-local的具体实现上有一些改动用来加速计算
  • 计算相关性矩阵的时候将channel数目减半
  • 计算相关性的时候不，枚举计算全局的点，可以通过pooling做降采样
• 训练的细节
  • 使用image-net的模型作为初始化
  • 只在non-local的最后输出加BN，其余地方都不加
• 调参试验
  • 关于f函数的选择？对结果影响不大
  • 把non-local块加在哪里?对结果影响不大，加在最后一层有轻微掉点
  • 加non-local块的数量？加的越多越好
  • 全局时间/全局空间/全局时空?将non-local单独应用于时间/空间均有提升，不过都不如应用于全局时空提升大
  • C2D+non-local与C3D作对比？C2D+non-local好
  • 将non-local应用于C3D?也可以获得提升
  • 加长时间维度？可以取得更好的效果

Abstract

In this paper we present non-local operations as a generic family of building blocks for capturing long-range dependencies

Intorduction

Repeating local operations has several limitations:

• it is computationally inefficient
• it causes optimization difficulties that need to be carefully addressed
• these challenges make multihop dependency modeling difficult

A non-local operation computes the response at a position as a weighted sum of the features at all positions in the input feature maps

There are several advantages of using non-local operations:

• In contrast to the progressive behavior of recurrent and convolutional operations, non-local operations capture long-range dependencies directly by computing interactions between any two positions, regardless of their positional distance
• As we show in experiments, non-local operations are efficient and achieve their best results even with only a few layers
• Finally, our non-local operations maintain the variable input sizes and can be easily combined with other operations

Related Work

skip-over

Non-local Neural Networks

Formulation

We define a generic non-local operation in deep neural networks as:

$$y_i= \frac {1} {C(x)}\sum_{\forall j}f(x_i, x_j)g(x_j)$$

• Here i is the index of an output position
• j is the index that enumerates all possible positions
• x is the input signal
• y is the output signal of the same size as x
• A pairwise function f computes a scalar (representing relationship such as affinity) between i and all j
• The unary function g computes a representation of the input signal at the position j
• The response is normalized by a factor C(x)

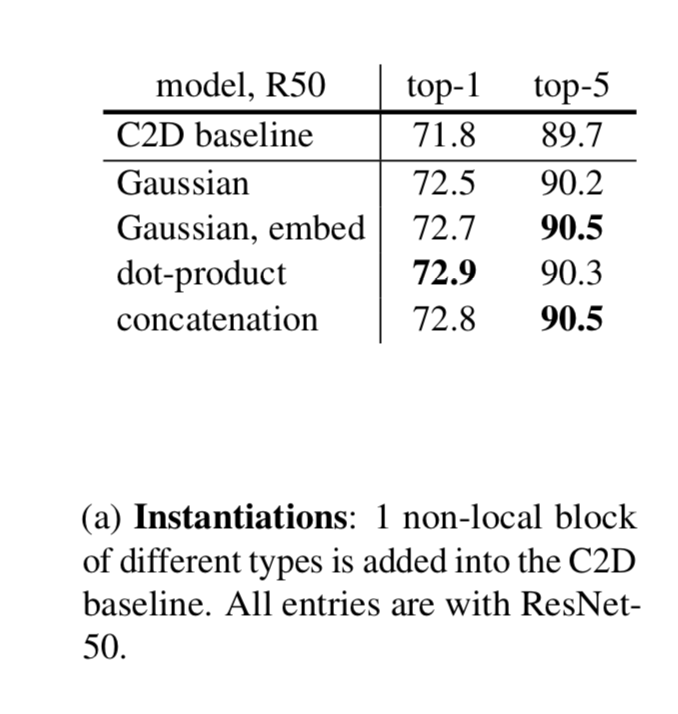
Instantiations

Next we describe several versions of f and g

Interestingly our non-local models are not sensitive to these choices

For simplicity, we only consider g in the form of a linear embedding

$$g(x_j) = W_gx_j$$

Next we discuss choices for the pairwise function f

Gaussian

$$f(x_i, x_j) = e^{x^T_ix_j}$$ $$C(x) = \sum_{\forall j}f(x_i, x_j)$$

Embedded Gaussian

$$f(x_i, x_j) = e^{\theta(x_i)^T\phi(x_j)}$$

Here $\theta(x_i) = W_\theta x_i$ and $\phi(x_j) = W_\phi x_j$ are two embeddings

$$C(x) = \sum_{\forall j}f(x_i, x_j)$$

We note that the self-attention module for a given i, $\frac 1 {C(x)}f(x_i, x_j)$ becomes the softmax computation.
Therefore self-attention is a special case of non-local operations in Embedded Gaussian version.
The attentional behavior is not essential in the applications we study

Dot puoduct

$$f(x_i, x_j) = \theta(x_i)^T\phi(x_j)$$

In this case, we set normalization factor as $C(x) = N$ where N is the number of positions in x, rather than the sum of f, because it simplifies gradient computation

Concatenation

$$f(x_i, x_j) = ReLU(w_f^T[\theta(x_i), \phi(x_j)])$$ $$C(x) = N$$

Non-local block

We define a non-local block as:

$$z_i = W_zy_i + x_i$$

where $y_i$ is output of non-local operation and $+x_i$ denotes a residual connection

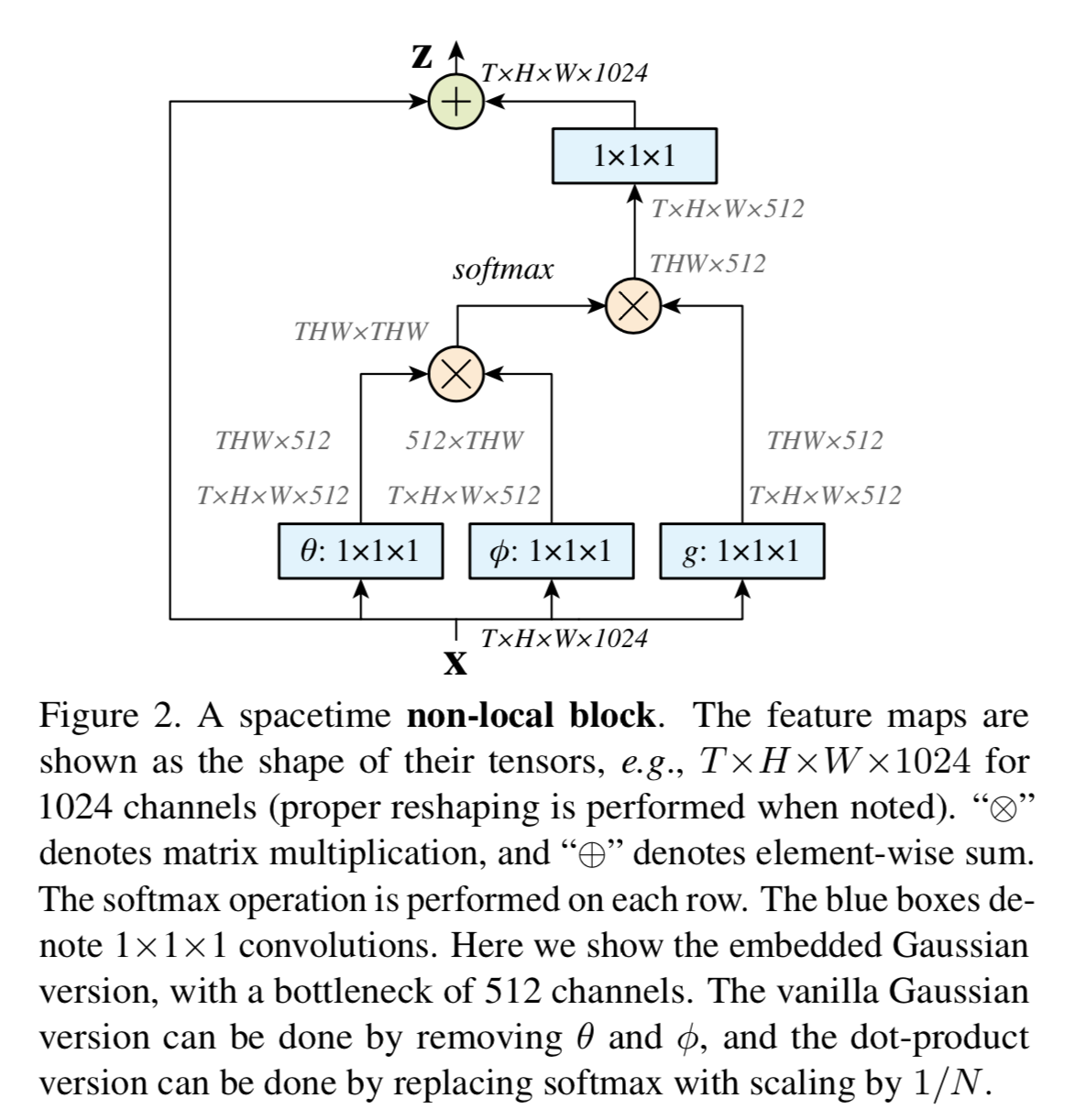
We further adopt the following implementations that make it more efficient

Implementation of Non-local blocks

We set the number of channels represented by $W_g, W_\theta,W_\phi$ to be half of the number of channels in x

We can change x to a subsampling version $\hat x$(e.g. by pooling)

Video Classification Models

First we describe our baseline network architectures for this task, and then extend them into 3D ConvNets and our proposed non-local nets

2D ConvNet baseline(C2D)

The only operation involving the temporal domain are the pooling layers

Inflated 3D ConvNet (I3D)

2D k×k kernel can be inflated as a 3D t×k×k kernel

Initialize: each of the t planes in the t×k×k kernel is initialized by the pre-trained k×k weights, rescaled by 1/t

Non-local network

We insert non-local blocks into C2D or I3D to turn them into non-local nets

The implementation details are described in the next section

Implementation Details

Traning

• pre-trained on ImageNet
• fine-tune our models using 32-frame input clips
• These clips are formed by randomly cropping out 64 consecutive frames from the original full-length video and then dropping every other frame
• We add a BN layer right after the last 1×1×1 layer that represents $W_z$ ; we do not add BN to other layers in a non-local block

Inference

For the temporal domain, in our practice we sample 10 clips evenly from a full-length video and compute the softmax scores on them individually. The final prediction is the averaged softmax scores of all clips

Experiments on Video Classification

Experiments on Kinetics

Instantiations

Interestingly, the embedded Gaussian, dot-product, and concatenation versions perform similarly

Our experiments show that the attentional (softmax) behavior of this module is not the key to the improvement in our applications; instead, it is more likely that the non-local behavior is important, and it is insensitive to the instantiations

In the rest of this paper, we use the embedded Gaussian version by default

Which stage to add non-local blocks?

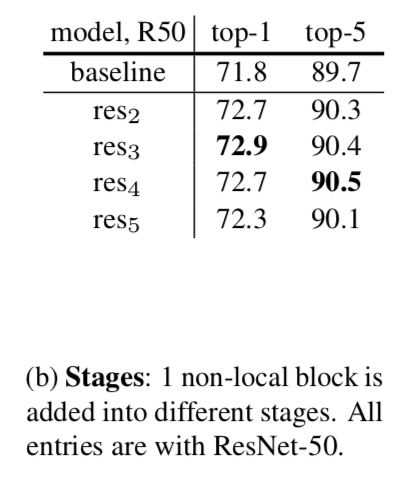
The improvement is similar

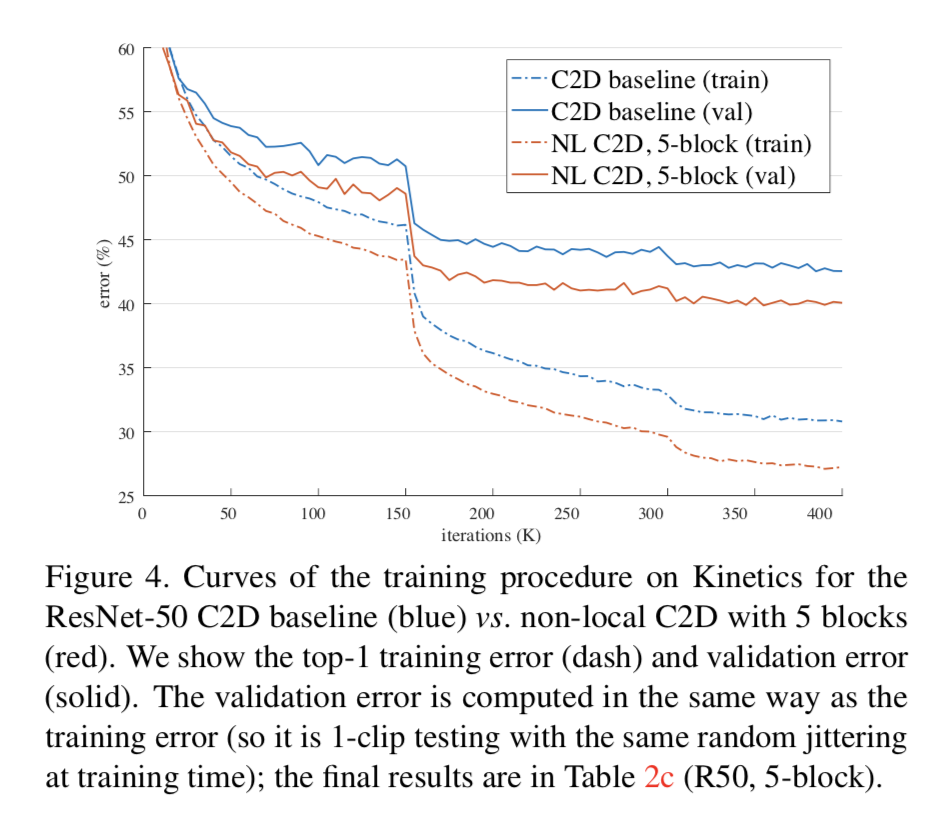
Going deeper with non-local blocks

This table shows the result of more non-local blocks

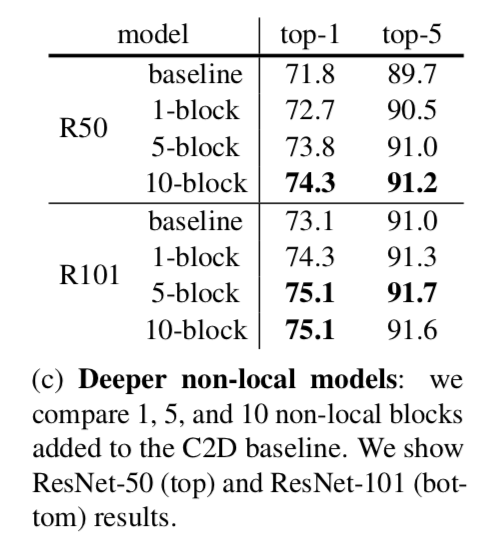
More non-local blocks in general lead to better results

Non-local in spacetime

This table we study the effect of non-local blocks applied along space, time or spacetime

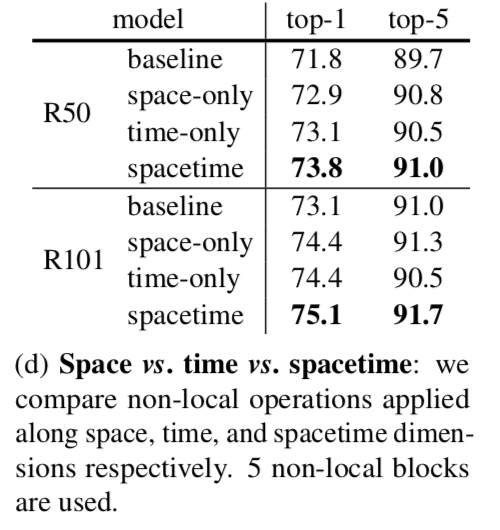
both the space-only and time-only versions improve over the C2D baseline, but are inferior to the spacetime version

Non-local net vs. 3D ConvNet

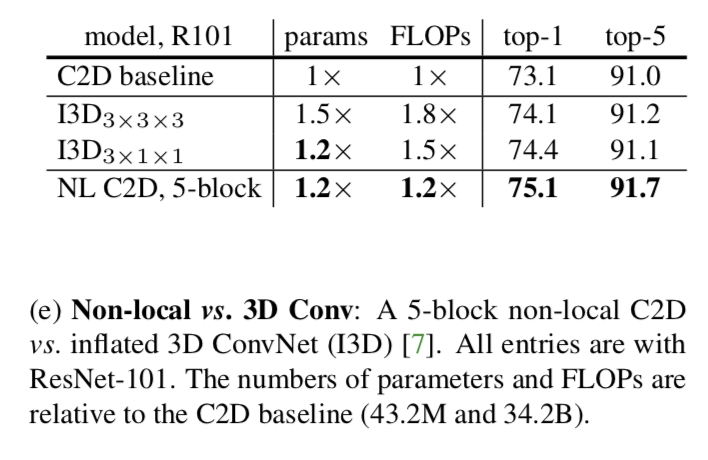
This comparison shows that our method can be more effective than 3D convolutions when used alone

Non-local 3D ConvNet

This table shows the results of inserting 5 blocks into I3D models

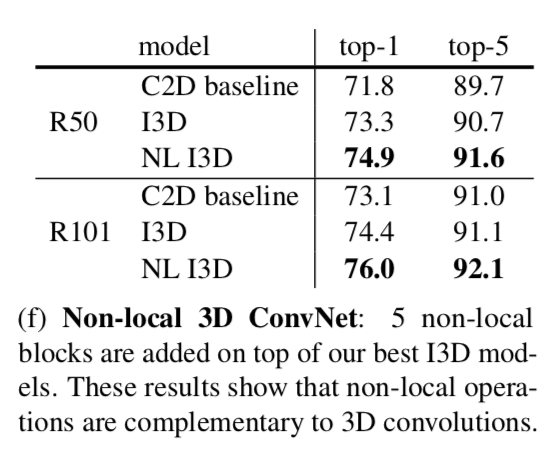
Shows that non-local operations and 3D convolutions are complementary

Longer sequences

Finally we investigate the generality of our models on longer input videos. We use input clips consisting of 128 consecutive frames without subsampling

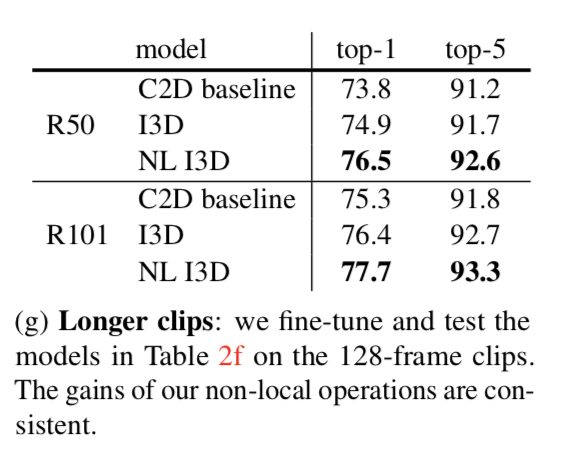
We also find that our NL I3D can maintain its gain over the I3D counterparts

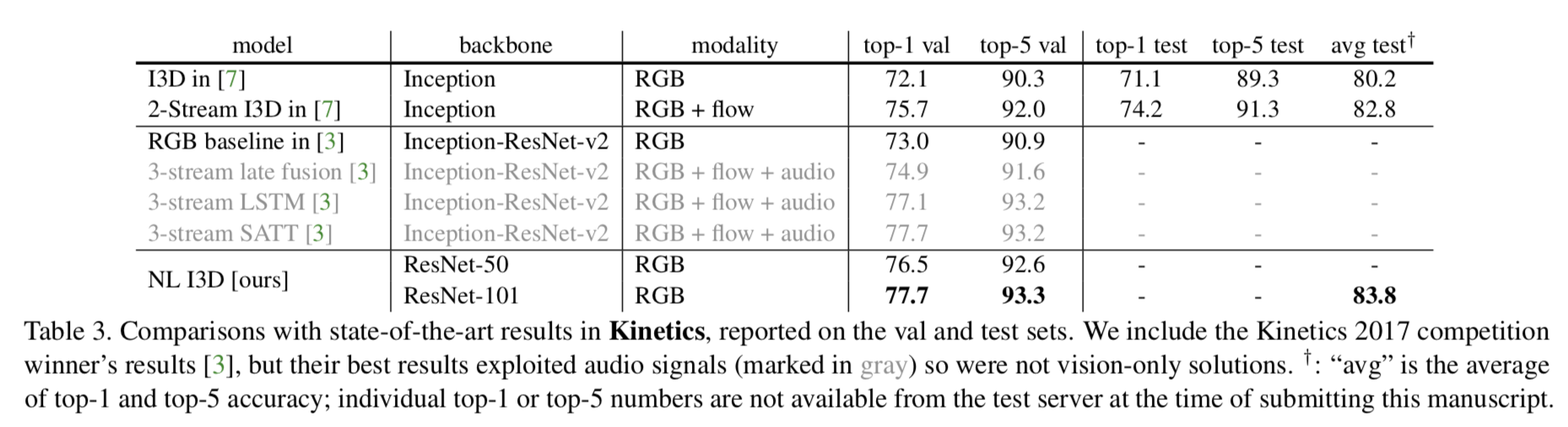
Comparisons with state-of-the-art results

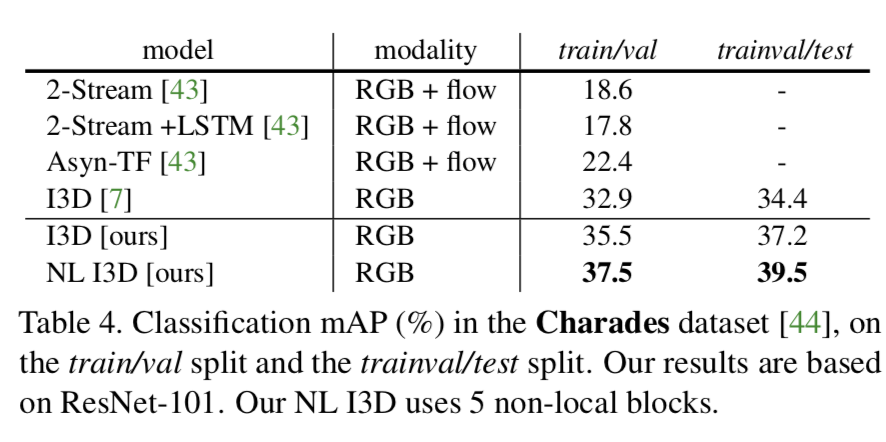
Experiments on Charades

Extension: Experiments on COCO

Object detection and instance segmentation

We modify the Mask R-CNN backbone by adding one non-local block

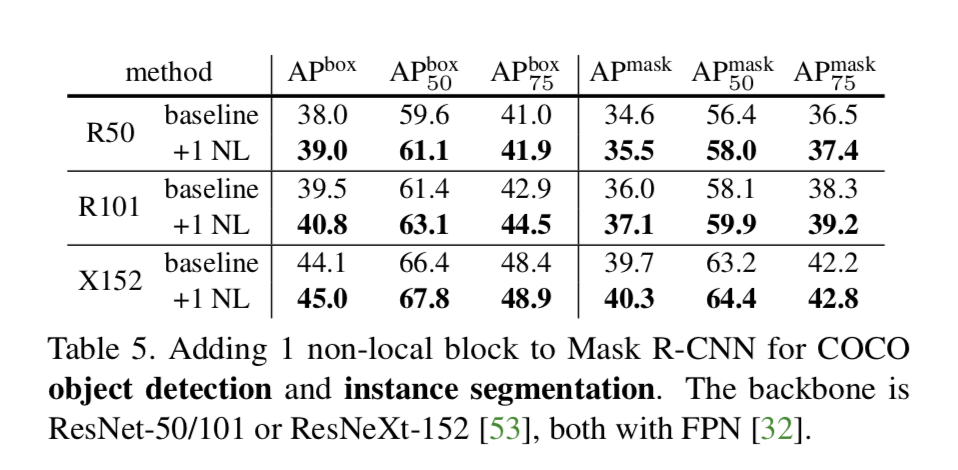
This comparison suggests that non-local dependency has not been sufficiently captured by existing models despite increased depth/capacity

Keypoint detection

Conclusion

skip-over