XGBoost

总结

• 在GBDT的基础上加了诸多创新点和工程化的东西达到了可以快速、分布式训练的目的
• 首先通过层层推导，利用泰勒展开的二阶项信息得到了一个判断分割点收益的方程： $$L_{split} = \frac {1} 2 [\frac {\sum_{i \in I_L}g_i^2} {\sum_{i \in {I_L}}(h_i + \lambda)} + \frac {\sum_{i \in I_R}g_i^2} {\sum_{i \in {I_R}}(h_i + \lambda)} - \frac {\sum_{i \in I}g_i^2} {\sum_{i \in {I}}(h_i + \lambda)}] - \gamma$$
• 提出了两个防止过拟合的方法
  • 新训练出的树所给出的预测结果需要乘上shrinkage因子再加到森林中去
  • 对于特征（列）做采样（等同于RF中的方法）
• 介绍了两种找最佳分割点的方法
  • 枚举所有分割点，然后找出最佳
  • 利用二阶导数信息当做权重，然后根据权重值来进行等权重划分，划分点即为分割点的候选点，然后依次遍历，此种方法可以应用于分布式计算
• 针对于稀疏数据，提出了学习default路径的思路，在枚举分割点的时候，将缺失的信息归到两个分支的其中一个，比较效果后决定default路径的方向
• 文章的工程化创新思路也非常多
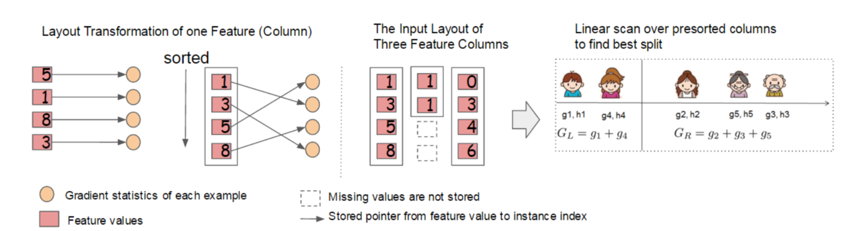
  • 针对树训练中所需的大量排序操作设计了Block结构，把每个特征按照特征值排序，存成索引。这样可以在计算前完成排序工作
  • 文章还针对CPU的cache机制进行了存储优化，主要是使CPU的访问地址尽量连续
  • 在内存不足时，设计了Out-of-core机制，过多的数据先写在硬盘上，在要用的时候由一个独立的线程预先加载进来，加大了训练数据的最大规模。在此基础上加入了，内容压缩，存储块共享技术，对训练过程提速
• 补充一些与传统GBM的区别
  • 使用了泰勒展开二阶项信息（牛顿法）计算下降方向
  • 不搜索步长
  • 加入正则项
  • 可以并行处理
  • 内置缺失值处理规则
  • 使用后剪枝而非预剪枝（GBM）

ABSTRACT

We propose a novel sparsity-aware algorithm for sparse data and weighted quantile sketch for approximate tree learning.

INTRODUCTION

factor of success is scalability in all scenarios

• a novel tree learning algorithm is for handling sparse data
• a theoretically justified weighted quantile sketch procedure enables handling instance weights in approximate tree learning
• We propose an effective cache-aware block structure for out-of-core tree learning.

we also make additional improvements in proposing a regularized learning objective

TREE BOOSTING IN A NUTSHELL

Regularized Learning Objective

$$L(\phi) = \sum_il(\hat {y_i}, y_i) + \sum_k\Omega(f_k)$$

Where $\Omega(f_k) = \gamma T + \frac {1} {2}\lambda||w||^2$
It penalizes the complexity of the model to avoid over-fitting

Gradient Tree Boosting

The model is trained in an additive manner:

$$L^{(t)} = \sum_{i = 1}^nl(y_i, \hat {y_i}^{(t - 1)} + f_t(x_i)) + \Omega(f_t)$$

Second-order approximation can be used to quickly optimize the objective:

$$L^{(t)} = \sum_{i = 1}^n[l(y_i, \hat y^{(t - 1)}) + g_if_t(x_i) + \frac {1} {2} h_if_t^2(x_i)] + \Omega(f_t)$$

where $g_i = \partial_{\hat y^{(t - 1)}}l(y_i, \hat y^{(t - 1)})$ and $h_i = \partial^2_{\hat y^{(t - 1)}}l(y_i, \hat y^{(t - 1)})$

define $I_j = \{i | q(x_i) = j\}$ as the instance set of leaf j, we rewrite L as follows:

$$\tilde L^{(t)} = \sum_{j = 1}^T[(\sum_{i \in I_j }g_i)w_j + \frac {1} {2}(\sum_{i \in I_j}h_i + \lambda)w_j^2] + \gamma T$$

for a fixed structure q(x), we can compute the optimal weight $w_j^*$ of j (set derivative of $w_j$ to 0):

$$w_j^* = - \frac {\sum_{i \in I_j}g_i} {\sum_{i \in I_j}h_i + \lambda}$$

and calculate the corresponding optimal value by:

$$\tilde L^{(t)} = - \frac {1} {2} \sum_{j = 1}^T \frac {\sum_{i \in I_j} g_i^2} {\sum_{i \in I_j} h_i + \lambda} + \gamma T$$

This equation can be used as a scoring function to measure the quality of a tree structure q

We can also give the function of the loss reduction after the split:

$$L_{split} = \frac {1} 2 [\frac {\sum_{i \in I_L}g_i^2} {\sum_{i \in {I_L}}(h_i + \lambda)} + \frac {\sum_{i \in I_R}g_i^2} {\sum_{i \in {I_R}}(h_i + \lambda)} - \frac {\sum_{i \in I}g_i^2} {\sum_{i \in {I}}(h_i + \lambda)}] - \gamma$$

Shrinkage and Column Subsampling

Prevent over-fitting:

• shrinkage
• column (feature) sub-sampling (better than row sub-sampling)

SPLIT FINDING ALGORITHMS

Basic Exact Greedy Algorithm

Approximate Algorithm

To support effective gradient tree boosting in:

• the data dose not fit entirely into memory
• distributed setting

we need an approximate algorithm:

• first proposes candidate splitting points according to percentiles of feature distribution
• then maps the continuous features into buckets split by these candidate points
• aggregates the statistics and finds the best solution among proposals based on the aggregated statistics

Weighted Quantile Sketch

define rank function:

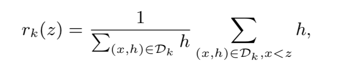
the goal is to find candidate split points $\{s_{k1}, s_{k2}, \dots, s_{kl}\}$, such that:

$$|r_k(s_{k, j}) - r_k(s_{k, j+1})| < \epsilon$$ $$s_{k, 1} = \underset {i} {min}x_{ik}, s_{k,l} = \underset {i} {max} x_{ik}$$

where $\epsilon$ is an approximation factor

Sparsity-aware Split Finding

We propose to add a default direction in each tree node

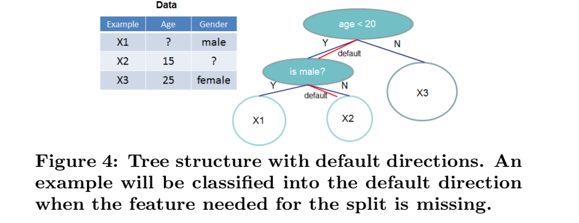
The key improvement is to only visit the non-missing entries $I_k$

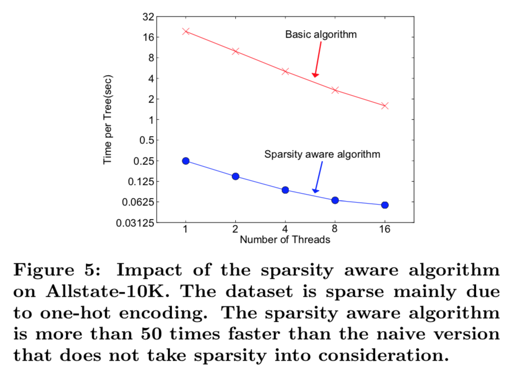
SYSTEM DESIGN

Column Block for Parallel Learning

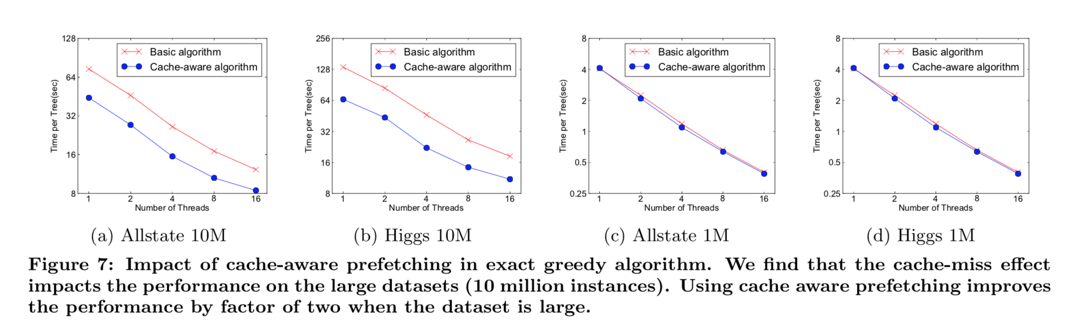
Cache-aware Access

we allocate an internal buffer in each thread, fetch the gradient statistics into it, and then perform accumulation in a mini-batch manner.

Blocks for Out-of-core Computation

During computation, it is important to use an independent thread to pre-fetch the block into a main memory buffer

It is important to reduce the overhead and increase the throughput of disk IO

We mainly use two techniques to improve the out-of-core computation:

• Block Compression
• Block Sharding

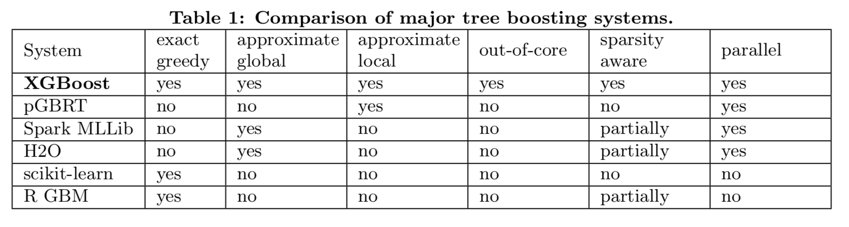
RELATED WORKS

END TO END EVALUATIONS

System Implementation

skip

Dataset and Setup

skip

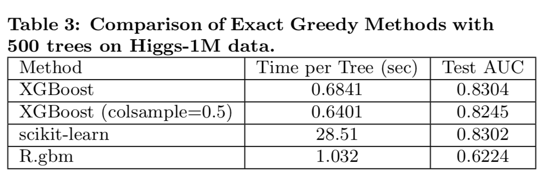
Classification

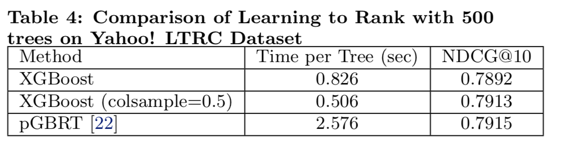
Learning to Rank

Out-of-core Experiment

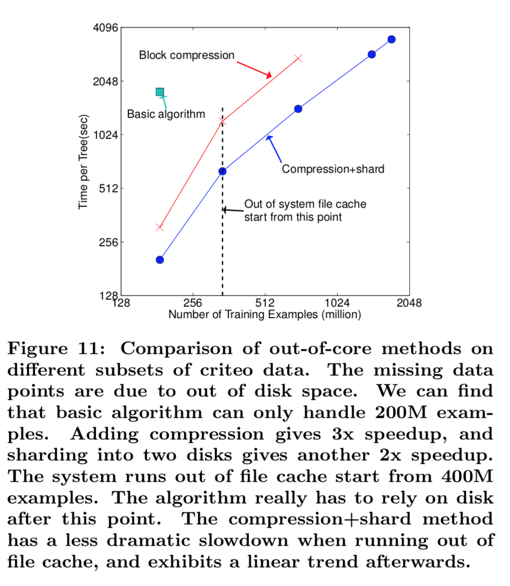
Distributed Experiment

It is able to take advantage of out-of-core computing and smoothly scale to all 1.7 billion examples

CONCLUSION

skip