GBDT = Gradient Boosting + Decision Tree
another names:
- MART(Multiple Additive Regression Tree)
- GBRT(Gradient Boosting Regression Tree)
- Tree Net
Ensemble learning
why ensemble?
- statistics
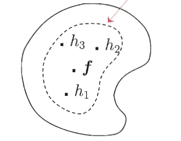
- calculation
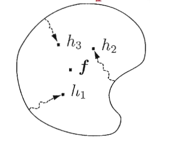
- representation
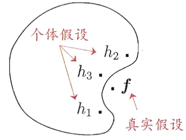
ensemble type
bagging
Bootstrap AGGregatING
train weak learner parallelly
low variance
boosting
train weak learner iteratively
low bias
- adaboosting
- gradient boosting
Gradient boosting
optimization in parameter space
optimization goal:
solution for the parameters in the form:
where $p_0$ is an initial guess and $\{P_m\}_1^m$ are successive increments (“steps” or “boosts”)
steepest-descent
define the increments $\{p_m\}_1^M$ as follows
- current gradient $g_m$ is computed
where - linear search learning rate
- the step is taken to be
optimization in function space
we consider $F(x)$ evaluated at each point x to be a “parameter” and seek to minimize
we take solution to be
where $f_0(x)$ is an initial guess, and $\{f_m(x)\}_1^M$ are incremental functions
current gradient:
and
the multiplier $\rho_m$ is given by the linear search
and the steepest-descent:
finite data
above approach breaks down when the joint distribution of (y, x) is represented by a finite data sample
and then
train gradient model by:
get learning rate $\beta$ by linear search
conclusion
