介绍
单变量的线性回归
线性回归损失函数
梯度下降
求使得损失函数最小的参数$w, b$
梯度下降需要同时更新所有参数

每个参数挨个更新的方法被称作Gauss-Seidel迭代
下降方向
下降方向由偏导数决定
偏导数的值只是提供了下降的方向,对下降多少没有准确指导意义(导数大,更新量大,反之亦然)
线性代数复习
矩阵乘法性质
- 不满足交换律
- 满足结合律
- 单位矩阵就是对角矩阵,在不同的上下文中有不同的维度

矩阵求逆
- 只有行列数相同的矩阵(方阵 square)才有逆矩阵
- $AA^{-1}=A^{-1}A=I$
- 求逆的方式是先求伴随矩阵(由代数余子式组成)然后除以矩阵行列式的值
- 不存在逆矩阵的矩阵称为奇异矩阵(singular)或者叫退化矩阵(degenerate)
- 不可逆条件——行列式为0
多变量相性回归
特征归一化
不做归一化会是收敛速度放缓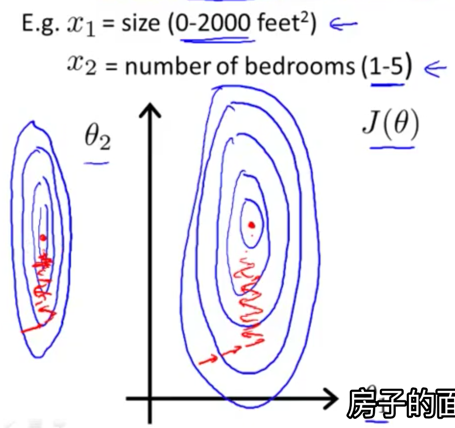
归一化方式
$X_i = \frac {X_i - {mean}_i} {max_i - min_i}$
梯度下降的一些细节
学习速率$\alpha$
- 当代价函数值随着迭代轮数慢慢下降时可以尝试更大的$\alpha$取得更快的收敛速度
- 当代价函数值随着迭代轮数指数上升(飞了)需要减小$\alpha$让梯度下降正常运行
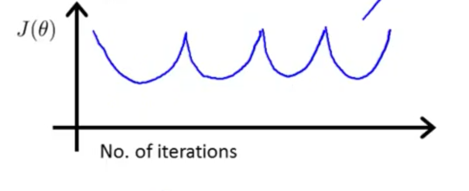
- 如果代价函数一会上升一会下降,一直反复,那么还是要减小$\alpha$
多项式回归
当直线并不能很好的拟合数据的时候,需要加一些0.5次项、2次项等等
用新的变量代替原来的多次变量形成新的多元线性回归式即可
正规方程
直接解出最优的$\theta$
在原特征前面加上1,用于方便的求解常数项
形成一个新的X
\begin{bmatrix}
1 & x_1^1 & x_1^2 & \dots & x_1^n \\
1 & x_2^1 & x_2^2 & \dots & x_2^n \\
& & \vdots \\
1 & x_m^1 & x_m^2 & \dots & x_m^n \\
\end{bmatrix}
可直接求解$\theta$
- 不需要做归一化了
- 不需要学习率
- 不需要迭代
- 在特征较多时速度慢($O(n^3)$时间复杂度 通常在n<1e4的时候选用)
$X^TX$不可逆
不可逆的直观原因
- 有多余的特征,两个特征之间满足一定的线性关系
- 删除相关性较高的特征
- 样本的数量少于特征的数量
- 减少特征数量
- 正规化
出现不可逆的情况是比较少见的,不用特别关注
Octave介绍
基本操作
- 注释: %
- 不等于: ~=
- 逻辑运算: && ||
- 改变控制台格式: PS1(‘>> ‘)
- 赋值语句后加分号,抑制输出
- disp只打印变量的值
- sprintf格式化输出
- format long/short 控制打印在屏幕上的数据的长短
- 矩阵声明
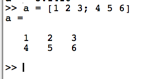
- 序列 start:step:end 返回一个行向量 默认step为1
- ones(row, col) 生成row行col列全是1的矩阵
- zero 全是0
- rand值为0~1的随机值
- randn符合正态分布的随机值
- eye(n) n*n 单位矩阵
- hist(矩阵,直方数)绘制直方图
- size(矩阵)返回矩阵的行和列
- length(矩阵)返回矩阵的最大维度
- help command 调取’command’的帮助信息
- who 显示所有变量,whos展示变量的更详尽信息
- clear 删除某个变量
- var(start:end)将[start,end]的变量从原数组中切片返回,下标从1开始
- var(row, col)返回var第row行col列元素
- ‘:’返回所有元素
- []表示数组,可以选取多行多列
- 直接在矩阵添加新的列(可把‘,’换为空格)
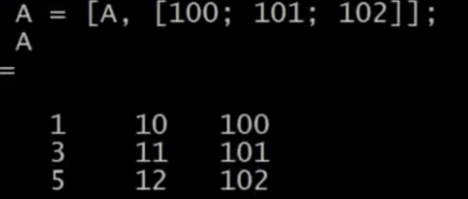
- 添加新的行的话把逗号换为分号
var(:) 将var中所有的变量当做列向量输出
可以直接使用一些bash指令
- pwd
- ls
exit,quit
数据导入导出
load file 将file的数据加载入Octave,赋值给一个新的变量,变量名为文件名去除扩展名
- save ‘file’ var 将var变量以’file’为名存储在硬盘上
- 加参数-ascii 将文件存为文本形式
数据运算
运算符
- A * B 矩阵乘法
- A .* B 矩阵对应元素相乘
- A .^ 2 矩阵每个元素平方
- 1 ./ A 矩阵每个元素的倒数
- A’ A的转置
- A < 3 对A做逻辑运算,返回bool矩阵
函数
- log(A)对于运算
- exp(A)指数运算
- abs(A)绝对值
- max(A)返回矩阵A中最大值,如果是接收返回值的是两个变量,那么返回最大值及其索引(从上往下,从左往右)
- find(A < 3) 将符合条件的bool矩阵变化为索引(从上往下,从左往右)。如果是接收返回值的是两个向量,那么返回索引被拆分为行向量和列向量
- magic(N) 生成N * N 的幻方
- sum(A) 将A的所有数字加和
- prod(A)将A的所有数字乘在一起
- floor(A)向下取整
- ceil(A)向上取整
- filpud 上下翻转
- pin 求逆
- pinv 伪求逆,适用于矩阵不可逆的情形
数据可视化
- plot(x, y): 横轴为X,纵轴为Y画图像
- 第三个参数可用’r’,’g’,’b’等表示画图的颜色
- hold on: 保留原图像,将旧图像画在新图像上面
- xlabel/ylabel: 为横轴纵轴加上文字说明
- lengend:加图例
- title:加图像标题
- print -dpng ‘pic.png’以png格式,pic为名保存图像
- close:关闭图像
- figure:指定当前绘图窗口
- subplot:
- 参数一,格子组列数
- 参数二,格子组行数
- 参数三,当前操作的格子
- axis(): 传入数组指定x轴最小值,x轴最大值,y轴最小值,y轴最大值
- clf: 清除图像
- imagesc(): 绘制矩阵彩色图
- colorbar: 展示颜色对应的数值
- colormap: 指定色彩空间
流程控制
- for
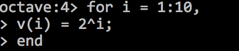
- 将for语句后面的变量变为数组效果一致
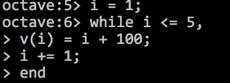
- while
- break
- 跳出循环
- if, elseif, else, end条件判断
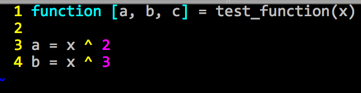
- 函数
- 要以”函数名.m”为名创建文件
- 文件中的函数名最好与文件名一致
- addpath命令增加函数的搜索路径
向量化
利用矩阵运算原理更高效的解决问题
逻辑回归
分类问题
额外的样本引起算法偏差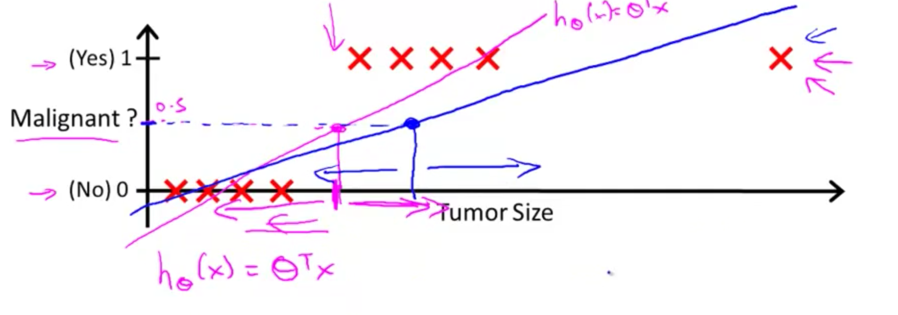
逻辑回归是分类算法
假设空间表达式
- sigmod函数
该函数的函数值得含义是
决策边界
决策边界是假设函数的一个属性
在决策边界内外的样本被划分为正/负样本
损失函数
直接将sidmod函数用作逻辑回归损失函数将导致损失函数非凸,用对数损失函数替代
该函数是关于$\theta$的凸函数
简化损失函数和梯度下降
统计学的最大似然估计法得到的损失函数
将上面的两部分合起来
全样本的损失函数
求偏导得到逻辑回归参数更新公式
此公式与现行回归的更新公式一模一样
区别在于逻辑回归中
线性回归中
进阶优化方法
- 共轭梯度法
- BFGS
- L-BFGS
高阶算法不需要手动指定学习速率$\alpha$
收敛速度更快
Octave提供了最小化函数值的模板
多分类问题
- one vs all(one vs rest):训练类别数目个分类器,分别代表属于其类别的先验概率,预测时取概率较大的当做分类结果
正则化
过拟合问题
过度拟合训练数据导致在真实数据的预测误差增大
模型从欠拟合到过拟合的过程中,模型偏差(bias)逐渐缩小,方差(variance)逐渐增大
处理过拟合的方式
- 减少特征数量
- 人工特征选择
- 自带特征选择的算法
- 正则化
惩罚项
在原始的损失函数后面加上
- 不惩罚常数项$\theta_0$(即使惩罚,差异也比较小)
- $\lambda$是正则化系数,平衡偏差与方差
惩罚项通常是L1,L2范数,均为闵可夫斯基距离的特例
- 当p = 1的时候又称为曼哈顿距离
- 当p = 2的时候又称为欧氏距离
- 当$x_j$为0向量时距离公式即为范数公式
线性回归正则化
- 将$\theta_0$与其他$\theta$参数分开更新
- 参数更新的表达式加上L2正则化项的偏导

- 每次更新都会把$\theta_j$变的更“小”一点
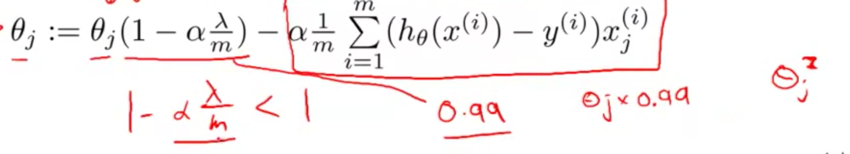
- 闭式解加正则化项是在X矩阵相乘之后加特征数+1维对角矩阵

- 加入正则化项还可以解决矩阵不可逆的问题
逻辑回归正则化
所加的正则项与线性回归的一致
神经网络展示
非线性假设
解决特征爆炸问题
自动特征交叉
神经和大脑
大脑的学习算法是泛化的,接各种传感器到任意皮层大脑都可以学着去使用它
神经网络表示
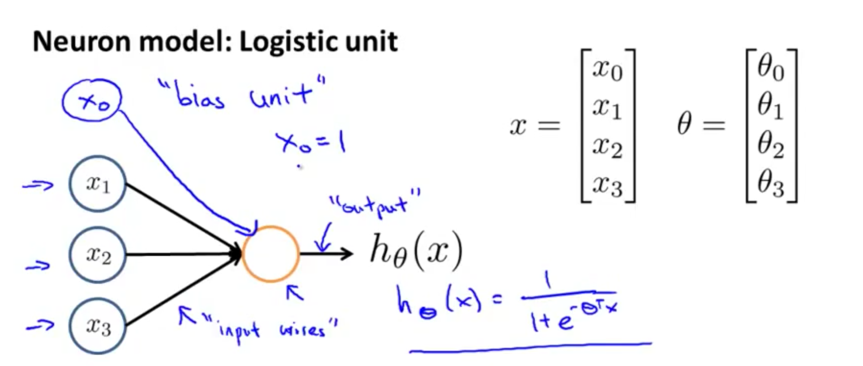
- first layer: input layer
- final layer: output layer
- other layer: hidden layer
1989年Robert Hecht-Nielsen证明了对于任何闭区间内的一个连续函数都可以用一个隐含层的BP网络来逼近,这就是万能逼近定理
隐藏层节点数目$h = \sqrt {m + n} + a$m为输入层节点数目,n为输出层节点数目,a为1~10之间的调节常数
神经网络表示第二弹
只有两层的神经网络其实就是逻辑回归
神经网络通过不同层之间的特征组合可以产生高阶特征
示例
与运算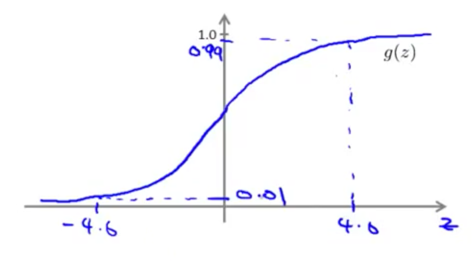
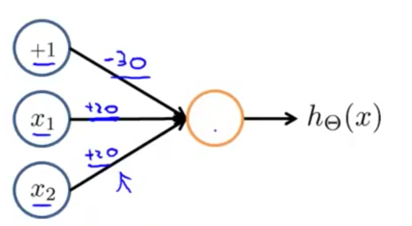
或运算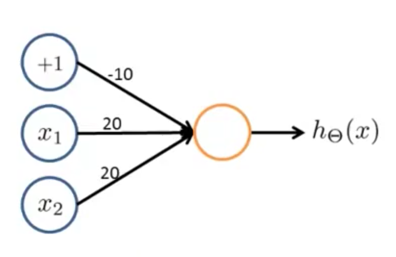
非运算
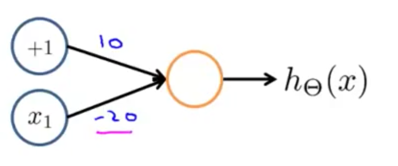
异或非运算
第二层由一个与运算,一个非与运算组成
非与运算: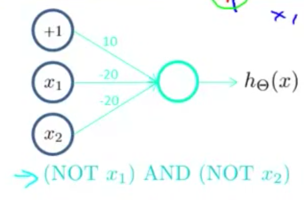
最终: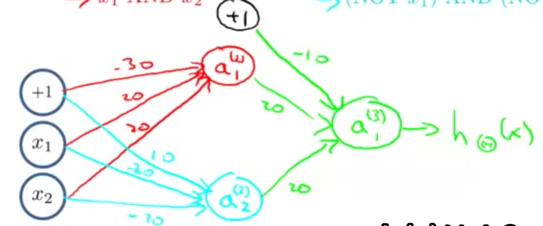
多分类
样本标记使用one-hot表示法
不能表示为
表示为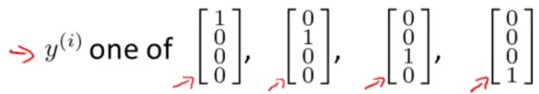
神经网络训练
损失函数
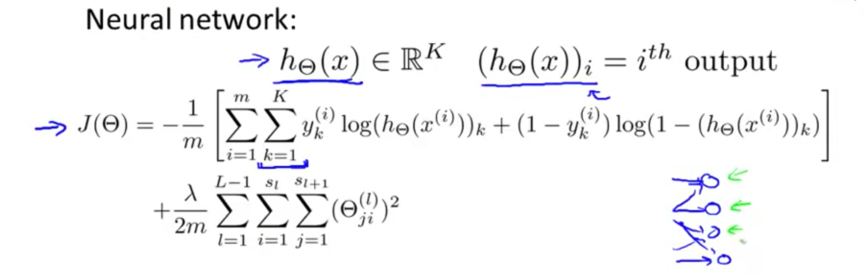
梯度项要考虑多分类的情况,将所有分类的误差累计
正则化项,将所有层的链接权重累计
反向传播算法
需要计算的方程式
- $J(\theta)$
- $\frac {\partial} {\partial\theta^{(j)}_{ij}}J(\theta)$
第一项求解通过正向传播算法逐步求解即可,
考虑如下结构网络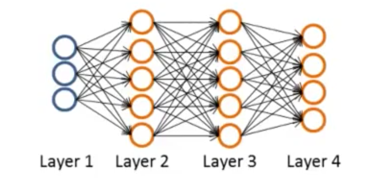
只有一个样本(x, y)的情形,正向传播的过程如下:
设定: $\delta^{(l)}_{j}$ = ‘error’ of node j in layer l
最后一层(L = 4)的误差为
$\delta^{(4)}_j = a^{(4)}_j - y_j$
用最后一层的误差反推之前的误差(不知道怎么来的,其实就是在计算偏导?)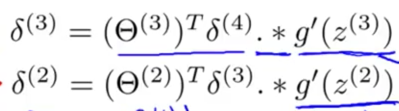
结论:
多样本时累计误差然后一次更新
对于偏差项的链接权重更新不加正则化项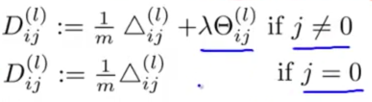

实际上$\delta$就是在求损失函数关于$z$的偏导
参数向量化

将多维的参数向量平铺为一个一维数组,然后再reshape生成需要的维数
梯度检验
梯度估计
- 当$\theta$是一个实数时又叫双侧拆分
通常$\epsilon = 10^{-4}$ - 当$\theta$是一个向量时
用类似的方法可得
检验流程
- 实现反向传播算法计算DVec
- 实现数值梯度检验计算gradApprox
- 确认两者之间相差不多(差几位小数)
- 去除第二步,直接使用反向传播训练神经网络
- 一定要在训练之前关闭检验流程,否则迭代将会变的非常缓慢
随机初始化
不能将所有权重都初始化为0。否则在训练过程中所有的隐藏层神经元计算的结果都是一致的,神经网络只能学到一个特征
一般是将权重随机初始化为$[-\epsilon, \epsilon]$之间的一个数字
整体架构
- 选择一种神经网络结构
- 确定输入层神经元数目(特征数)
- 确定输出层神经元数目(分类数量)
- 隐藏层数目默认为1,通常来说隐藏层越多越好
- 如果隐藏层数目多于1个,那么所有隐藏层的神经元数目应该相同
- 训练神经网络
- 随机初始化权重
- 实现正向传播代码
- 实现损失函数计算代码
- 实现反向传播代码
- 遍历所有样本进行训练
- 使用梯度检验流程验证反向传播算法所计算的梯度的正确性;验证通过后关闭检验流程
- 使用梯度下降或者更高级的方法配合反向传播来减小损失函数$J(\theta)$的值;由于$J(\theta)$是非凸函数,所以有可能停留在局部最优(但其实无所谓?)
无人驾驶应用
一段视频……
对于应用机器学习的一些建议
如何选择系统的改进方向
当你发现训练出的模型在新的数据集上表现的很糟糕,几种选择如下:
- 收集更多的训练数据
- 减特征,防止过拟合
- 加特征
- 加高阶特征,例如$x_1^2, x_1x_2$
- 调整正则化项系数
如何在他们之中做出选择是解决问题的关键
围绕这些问题所产生的一系列方法称为机器学习诊断法
评估假设函数
单纯用训练集loss不能表征模型的好坏
需要将训练集分成两部分(通常来说训练数据占7,测试数据占3)
如果数据是有序的,那么在生成数据集的时候需要随机抽取
模型选择
通过测试集的表现来选择模型的超参的之后,就不能使用测试集去评估模型的泛化能力了(因为选出来的就是测试集的误差最小者)
为解决这种问题将数据集合多分出来一份——交叉验证集(训练:交叉:测试 = 3 : 1 : 1)
使用交叉验证集选择模型的超参,再通测试集验证泛化性能
偏差和方差
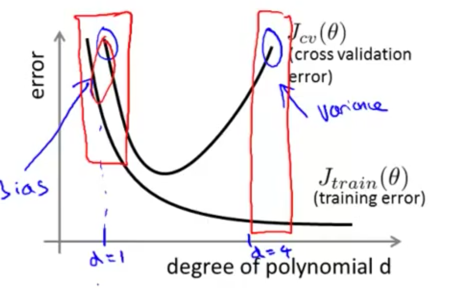
高偏差时训练集误差很大,测试误差也很大
高方差时训练集误差很小,测试误差很大
正则化项
通过引入正则化项可以有效缓解过拟合的情况,从而降低偏差
随着正则化项的增大,方差增大,交叉验证集loss增大,通过交叉验证集确定合适的$\lambda$取值,然后通过测试集验证模型的泛化性能
学习曲线
用于判断算法是否处于偏差、方差或者两者都有
高偏差情形
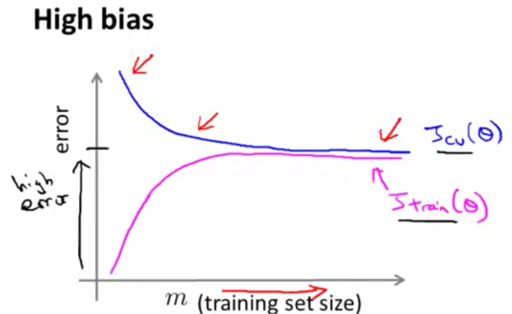
当模型处于高偏差状态下时,增加训练样本对于增加模型的拟合程度无益(例如用直线去拟合曲线)
高方差情形

当训练误差与交叉验证集误差中间有较大距离时模型处于高方差情形
当模型处于高方差状态下时增加训练样本应该会有帮助
解决方案
高偏差时
- 增加特征个数
- 增加高阶特征
- 减小正则化系数
- (使用神经网络时)增加神经元个数,增加神经元层数
高方差时
- 增加训练样本
- 减少特征个数
- 增加正则化系数
- (使用神经网络时)减少神经元个数,减少神经元层数
机器学习系统设计
确立优先级
以反垃圾邮件的例子
首先确立特征——特定单词是否出现
- 收集大量的数据
- honeypot 项目
- 特征工程,构建复杂特征
- 构建算法检测拼写错误
头脑风暴,找点子
误差分析
推荐方案
- 快速制作一个base line方法,用交叉验证检验
- 绘制学习曲线,判断是否需要增加数据/特征
- 人肉检查bad case,总结bad case的分类错误缘由——指导增加新特征or修正系统漏洞
用数据说话,通过量化指标指导决策
快速尝试,快速迭代
数据倾斜的误差度量
数据中一类数据比另一类数据多很多,造成单纯的预估成某一类就可以获得很低的错误率。
为解决此类问题提出新的度量方式
准确率/召回率
准确率为 True Pos / (True Pos + False Pos)
召回率为 True Pos / (True Pos + False Neg)
平衡准确率&召回率
调整sigmod函数阈值
将预测为正例的阈值调高会增加准确率,降低召回率反之亦然
F1度量
和简单的算术平均相比,这个分数更侧重P和R的均衡,两者的值不能相差过大才能计算得出较高的结果
机器学习之中的训练数据
在使用低偏差模型的时候,用大量的数据有助于减小测试集误差
支持向量机
最优化目标
对于逻辑回归中的损失函数,用直线逼近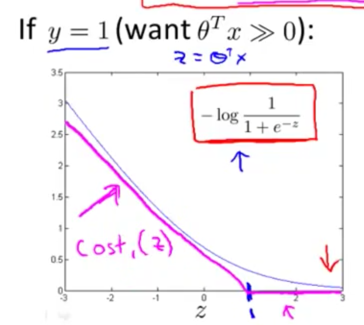
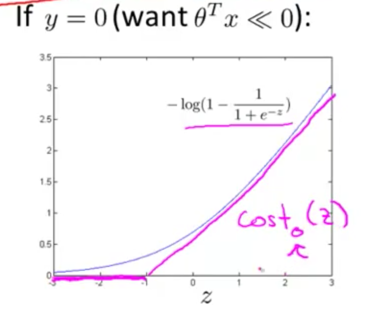
如两图中紫红色的线
SVM中用两个近似损失函数值代替逻辑回归中的损失项,得到新的损失函数
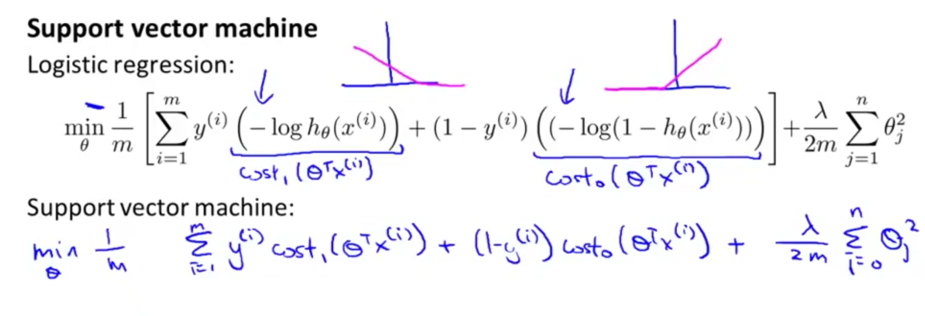
变化常数项
变化为hinge 损失函数:
最大间距
SVM会将决策边界设立在里两类样本点尽量远的地方
由于损失函数的定义
- 当$y = 1, \theta^TX >= 1$(不仅仅>=0)时损失函数为0(比逻辑回归的损失函数值小)
- 反之当$y = 0, \theta^TX <= -1$(不仅仅<0)时损失函数也为0
- 这样人为划出一块损失函数为0的区间,这个区间就是SVM决策边间出现的主要原因
离群点处理
损失函数中的系数C就是调节训练样本正确性和正则化项之间平衡的系数
当系数C比较大时,模型倾向于拟合所有训练样本,当C较小时,模型倾向于系数向量的简介,后者对于利群点的鲁棒性有较大的优势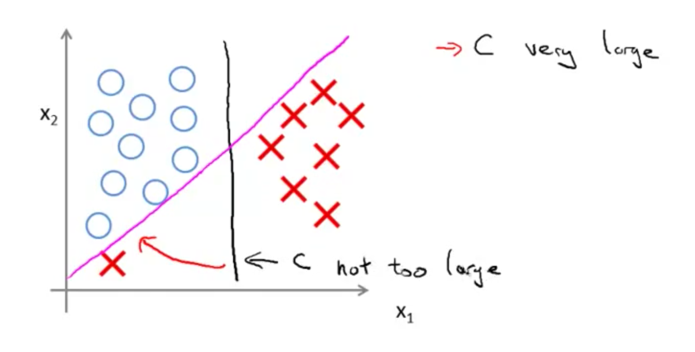
最大间距背后的数学解释
根据向量长度的定义,SVM的正则化项(二阶范数)可以表示为参数向量模的平方
当要求把全部样本正确分类的时候,目标方程可简写为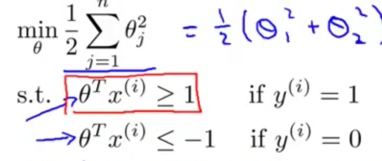
将$\theta^Tx^{(i)}$看做$\theta$和$x^{(i)}$两个向量的內积,由于对于內积的大小有要求,不仅仅是以0为分界,所以决策边界会相对于两侧的样本留出一定的空隙
$\theta$向量与决策边界总是正交的,由图可见阈值对于决策边界的影响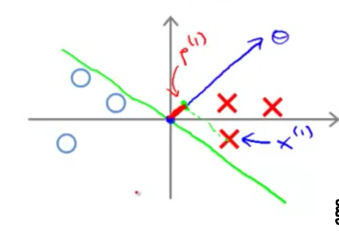
图中红线标示出来的就是虽然內积为正,但是內积的大小并不满足要求的情况
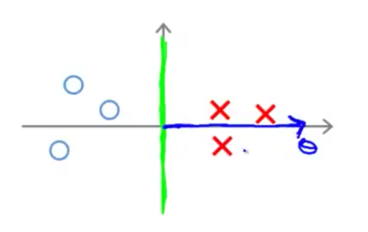
决策边界改为下图的形式的话即可满足要求
核函数
面对线性不可分的问题,需要使用高阶特征
高阶特征可由原始特征映射过去,这种映射的过程被称为核函数
核函数的种类很多,例如高斯核函数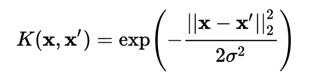
刻画两个向量的相似度,越相似值越接近1,反之接近0
$\sigma$参数控制从1下降到0的速度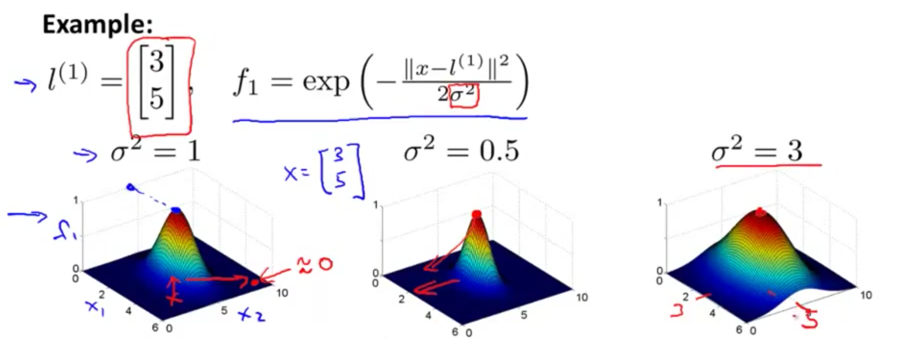
越大下降越缓慢
利用这种相似性,可以配合标记点构造比较复杂的决策边界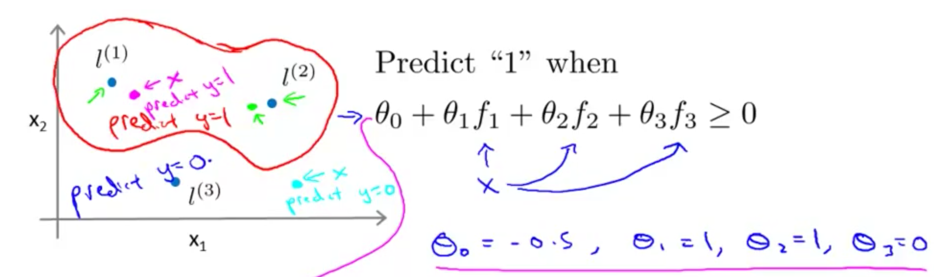
标记点的选择
首先将标记点标在于训练样本完全重合的地方
然后通过高斯核函数得到新的特征向量(m+1维,m为样本数量)
改写损失函数,用新特征代入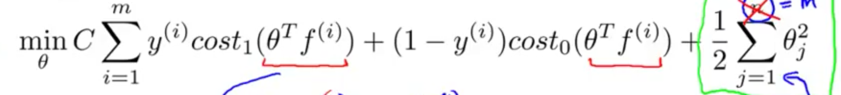
然后训练求解即可
SVM中的超参
- C:
较大的C:低偏差,高方差
较小的C:高偏差,低方差 - $\sigma$
大:特征向量的值会较为平滑,高偏差,低方差
小:低偏差,高方差
SVM应用
准备工作
- 依照偏差、方差去选择超参C
- 选择核函数or不使用核函数(线性核函数);当特征维度较大,数据量较小的时候最好使用线性核函数
- 如果选择了高斯核函数,那么需要确定参数$\sigma$还是参照方差、偏差选择
- 使用核函数之前做特征归一化
- 如果选择其他的核函数或者自定义核函数,那么该核函数需要满足莫塞尔定理
- 多项式核函数:$k(x, l) = (x^Tl + m)^n$
- 字符串核函数:输入的文本是字符串
- 卡方核函数
- 直方图交叉核函数
多分类问题,使用one vs all方法训练k个分类器,选取预测结果最高的类别作为预测结果
LR 对比 SVM
n是特征数量,m是样本数量
- 当n相对于m很大时使用LR或者线性核
- 当n很小,m适中(n = 1~1000,m = 10~10000)时用高斯核SVM
- 当n很小,m很大时,尝试增加特征数量,使用LR或者线性核
调试模型的方法比选用某个模型更加重要
聚类
无监督学习
只有x值没有标签
应用之一——聚类
k-means
K-均值算法
将一组没有加标签的样本分为m类
- 随机选择m个点作为类中心
- 遍历每一个样本点,将样本点分给离他最近的类中心
- 将每个类的类中心改为该类中所有点的坐标的均值然后回到第2步直到样本归属无更改
- 如果在簇中心移动的过程中有某一类没有任何样本点,那么直接将这一类删除,视情况是否新随机出一个簇
优化目标
变量定义
优化目标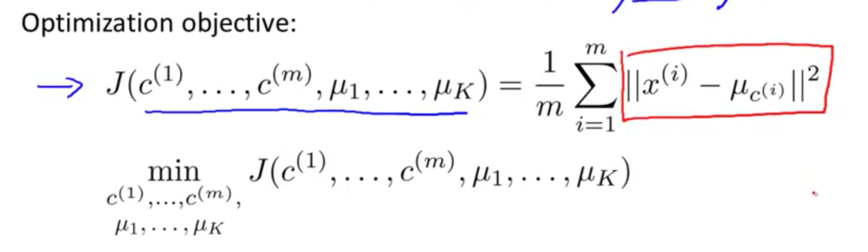
即每个样本点距他所属的类别的质心距离最短
初始化质心
随机选择
- 首先质心的数量要小于样本数量
- 随机选择k个样本作为质心
随机初始化容易陷入局部最优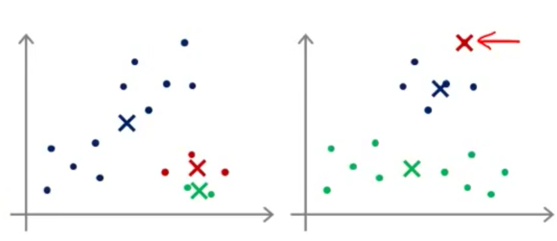
一般通过多次随机取得最小值,次数一般在50~1000之间
随机选择方法适用于k的类数不大的情形2-10
选择聚类数目
手动选择
肘部法则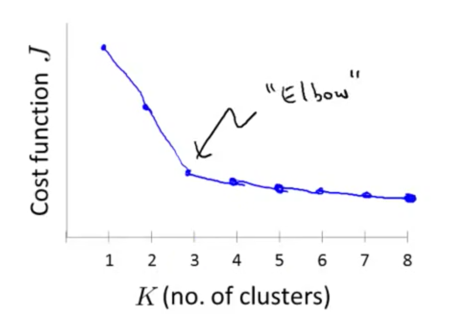
根据递增的K画出代价函数曲线
会发现一个明显的拐点,越过这个拐点之后损失函数的值会下降的越来越缓慢,这个拐点就是最佳的聚类数目选择值
但是情况有时候不那么理想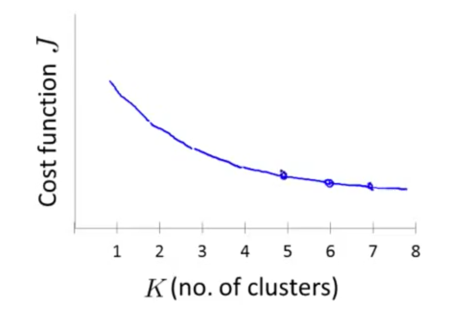
按照业务逻辑手动选择k
降维
数据压缩
通过去除相关性很强的特征,节省空间,算法提速
数据可视化
N维降到2维
PCA
Principal Componet Analysis —— 主成分分析法
主要做的是寻找一个低维空间,将现有数据投影到上面所需的距离最短
低维空间用向量表示,正负无关
与线性回归比较,线性回归的损失函数是预测值与真实值得比较: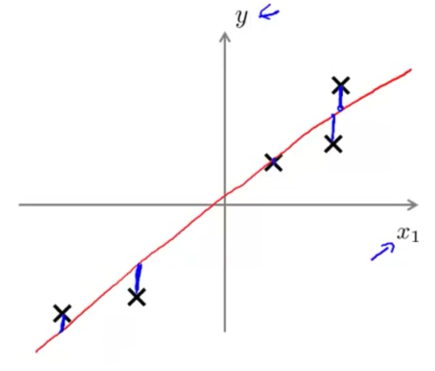
PCA是真实数据与投射空间的距离: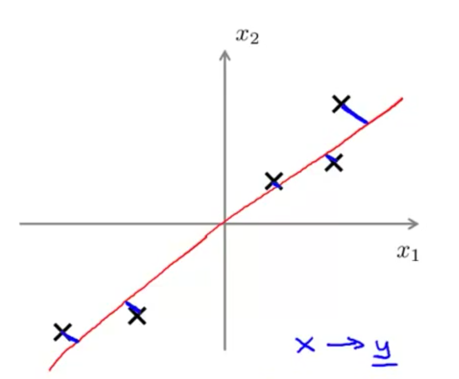
训练过程
- 数据归一化
- 假定将数据从N维降维到K维,需计算协方差矩阵:
- 通过SVD计算特征向量
- 取其中NN的矩阵U的前K列生成NK的矩阵$U_{reduce}$
- 映射过后的值为$z = U_{reduce}^T * x$
主成分数量选择
主要原则: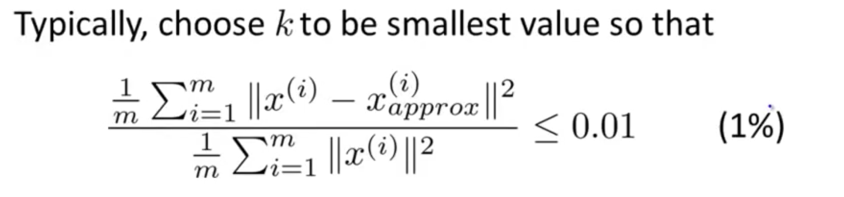
让数据的变化尽可能小
这个数字可以通过SVD产生的S矩阵进行简便计算: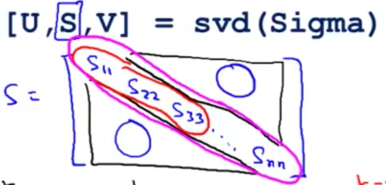
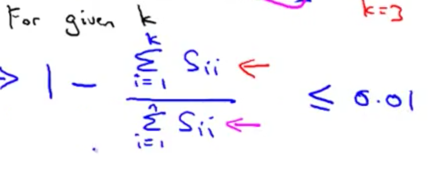
压缩还原
还原出来的数据还是在高维空间的低维空间中: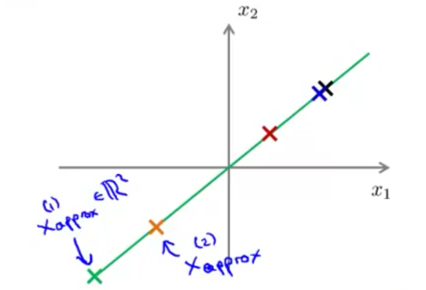
应用
对于高维特征可用PCA降维之后计算
对训练集和测试集做同样的处理
数据压缩:
- 节省内存和磁盘空间占用
- 加速学习速率
可视化:
- 降到2维或者3维绘图
不要用PCA来防止过拟合,效果不如正则化好,另外PCA降维没有用到标签信息,更加容易舍弃有价值的信息
默认不要使用PCA,只有当确定除了某种问题的时候再使用它去解决特征的问题
异态检测
概述
通过收集关键特征的值,检测是否存在离群点
或者给定一个点是否是离群点
高斯分布
x服从均值为$\mu$方差为$\sigma^2$的高斯分布记作:
概率密度函数为
分布的参数估计
算法部分
计算事件发生概率:
$P(x) = \prod^n_{j = 1}P(x_i;\mu_j,\sigma^2_j)$
步骤:
- 选择特征
- 通过训练数据训练特征的高斯分布超参
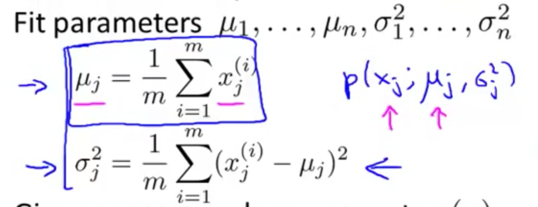
- 对于新的预测样本给出其发生的概率,如果概率小于阈值那么认定为异常样本
特征选择
将样本上的特征画图,看是否符合高斯分布的曲线形状,如果符合那么可以加入异态检测特征集合
如果特征的分布不服从高斯分布,那么通过变换(log、幂运算)转换
多元高斯分布
用于检测在单个特征上看起来都非常正常,实际将特征组合起来已经离群的异常点
不将特征独立考虑,一次性将概率密度函数建模,将原来的方差换为协方差矩阵,写作
其中$\Sigma$是n*n的协方差矩阵
参数估计
协方差矩阵: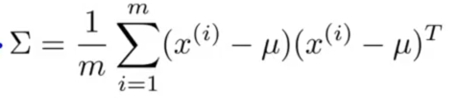
当协方差矩阵不可逆时,检查冗余特征
其余预测与高斯分布一致
高斯分布的等高线是沿着轴线方向,协方差矩阵是对角矩阵,需要自己创造特征表示多个特征之间的联系
与高斯分布相比,多元高斯分布:
- 能够表示特征之间的线性关系
- 当m数量小于特征数量的时候不能正常工作,通常样本数量大于10倍的特征数量
- 计算复杂
推荐系统
机器学习最重要的应用之一
特征作为机器学习的一个重要参数,有一些算法可以自动学习特征量,推荐系统就是这种算法的一种应用
问题建模
对于一个用户对电影打分的场景
变量定义:
用户给一些电影打了分,有些没打,预测用户没打分的电影会打多少分
基于内容的推荐
将电影本身按照内容分类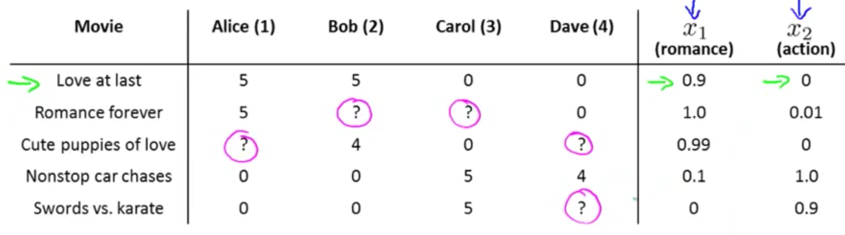
提取n个特征为电影打分
预测的流程为,为每个用户训练一个n+1维特征向量,每个电影在前面拼上一个常数1,也形成一个n+1维向量,两个向量的点积就是用户对于新电影的评分
拓展问题的定义:
训练向量的过程使用最小二乘回归,加正则项: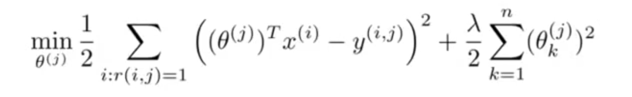
梯度下降进行学习: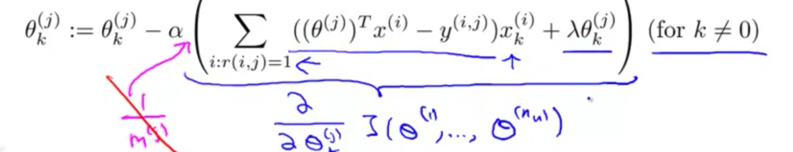
协同过滤
人工打标签的难度较大,难以完成
将问题的场景进行转换,先给定用户的偏好,然后去学习电影的特征向量
优化目标: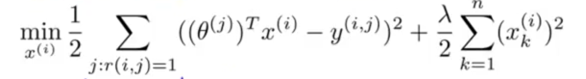
以此来计算电影的特征向量
用户与电影之间的向量可以相互推导: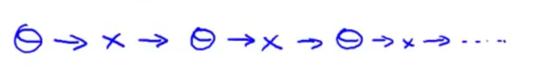
可以先给定一个随机$\theta$然后训练直到收敛
这就是基本的协同过滤算法(思想类似EM)
改进版
将用户特征向量优化目标与电影特征向量的损失函数相加,得到新的损失函数,直接求解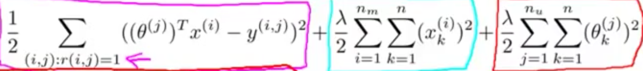
注意 此特征向量的长度为n,不再有偏置项
算法步骤:
- 初始化用户特征参数和电影特征参数
- 使用梯度下降或者其他优化算法对参数进行求解(用户特征和电影特征用不同的偏导求解)
- 预测使用用户特征向量和电影特征向量做点积
向量化实现
将电影特征组成矩阵X: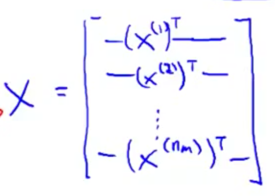
将用户特征组成矩阵$\theta$: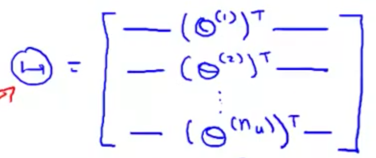
将矩阵相乘得到每个用户对于每个电影打分的结果矩阵
因为得到的矩阵是低秩矩阵,所以改算法又被称为低秩矩阵分解
挖掘相似产品
通过计算产品特征向量之间的距离
运行细节——均值归一化
假设存在一个用户,他对所有的商品均没有评分,那么依据正则化项的约束,他将所有的向量值都置为0,为避免这种为题,一般需要将矩阵进行均值归一化操作
原矩阵: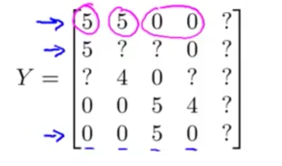
减去均值,得到归一化矩阵: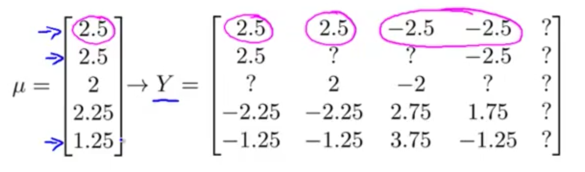
在训练得到预测矩阵之后将均值加回,就使得未预测用户的评分都是均值
大规模数据挖掘
大数据学习
在使用大数据集进行训练的时候会产生诸如计算量大等问题,这个时候需要考虑是否真的需要考虑真的需要使用这么大的数据量,如果测试集和训练集的误差存在较大gap那么增加数据量的做法应该有用,否则考虑减小数据量(就目前的经验来说都是无脑加数据就好,没有计算时间上的瓶颈)
随机梯度下降
- 对样本集进行随机重排序
- 然后对每个样本计算梯度,立刻更新参数
- 遍历所有样本一遍,学习完成
- 重复上述过程1~10次
随机梯度下降一般不会收敛在全局最小值上,会在其很近的地方波动,可以通过动态学习率的方式缓解:
学习率随着迭代次数的增加而减小
小批量梯度下降
每次使用b个样本计算梯度更新参数
对比随机梯度下降,这种计算方式可以向量化、并行化计算
有个缺点是多了一个额外的参数b
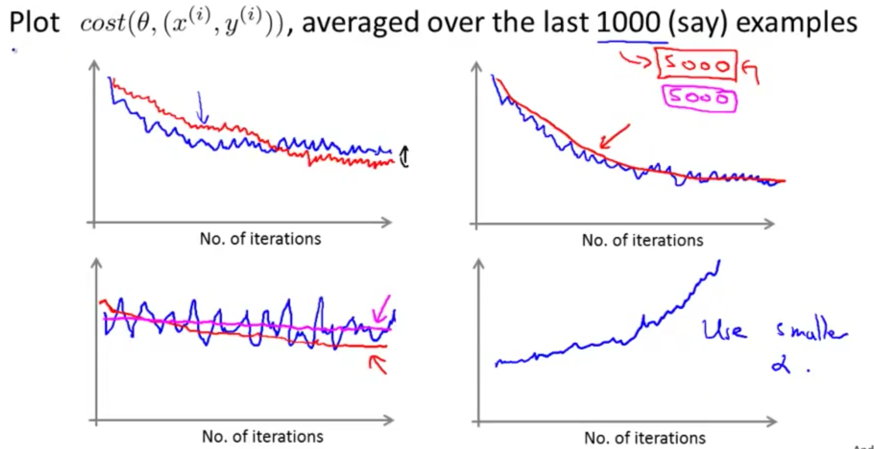
收敛性检测
在使用特定样本进行学习之前,先计算该样本的误差,然后每1000个样本画出误差曲线观察
如果误差曲线抖动比较剧烈,那么加大平均样本数量会减小这种波动,
在线学习
对于持续高频产生新数据的行为都可以应用在线学习进行建模
MR和并行化
Map-Reduce
分治思想,将数据分为多份,分别处理,然后将结果汇总,进行计算输出
并行化
单机多核,同理MR
OCR应用
光学字符识别,从照片中抠出文字
主要步骤
算法步骤
- 从图像中检测文字
- 字符切分
- 字符识别
上述步骤构成了整个系统的算法流水线
滑动窗
滑动窗(sliding window)是检测图像中物体的常用算法,文字的检测长宽比不固定,相比较而言,行人检测简单一些,先以行人检测为例
先通过网络获取固定长宽(86 * 32)的正负样本
负样本:
正样本:
- 以86 * 32 为窗口,滑动截取图片成若干个小方块,通过模型预测这些窗口的图片是否含有行人
- 每次窗口滑动的大小称为step size(步长)
- 将窗口放大,再将图片分割为若干块,将图片resize成原始分类器大小(86 * 32)后再传入分类器
- 再放大重复以上步骤
回到文字检测的问题上来
- 我们同样使用固定长宽的方块去检测单个字符
- 用字符训练数据训练模型
- 用模型检测图片上是包含字符,生成二值图

- 使用拓展算法将孤立的白色方块连成一片

- 加策略进行数据清洗,将瘦高的连通域丢弃
- 训练字符分割点模型,检测在哪里应该将两个字符分开,然后一维滑动窗口遍历整个连通域,将字符图片切割
- 训练字符识别模型,将所有单体字符识别出来
人工合成数据
- 通过不同的字体类型 + 不同背景直接创造数据集
- 通过真实数据 + 扭曲变形/干扰制造额外数据
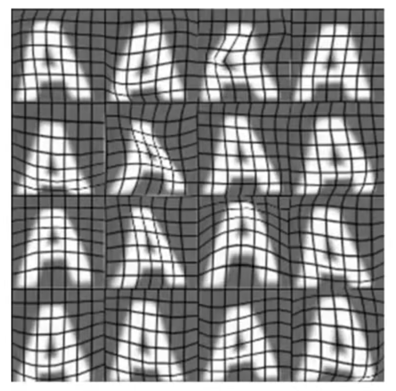
- 加干扰数据的时候应该注意,所做变换信息应该是现实(测试集)中可能出现的情景,不要直接加纯随机和噪声
- 在造数据之前最好先确定已经有一个低偏差模型
- 如何通过人工的方式获取大量数据是一个提升算法性能比较关键的点
- 自己收集&标记数据也是一个扩展数据的方法,评估人工收集数据的成本
- 众包收集数据
上限分析
分析整个系统中的瓶颈是在哪里
依次让各个模块输出标准答案,测试系统的准确率是多少
根据数据得出改进某些模块的增益