Learning to Rank using Gradient Descent

总结

通过本篇文章，笔者第一次接触到Pair-wise训练
其实总体来看实现思路非常简单，就是通过两个point分别过模型inference然后对结果做差，将diff当做一个样本在另外一个样本之前（记$ahead_{ij}$）的对数几率，将这个几率再过一遍Sigmod函数，就得到了概率值(记$P(ahead_{ij})$)
文章很大的篇幅，证明了做差之后结果是可导的，这对模型训练至关重要，但被我可耻的跳过了……
大篇幅的证明 + 只改动几行代码的实现（对于自动求导的神经网络来说是这样的）和之前读的W-GAN感觉很像
不管怎么说Pair-wise训练算是摸到点门道了

Introduction

cast the ranking problem as an ordinal regression problem is to solve an unnecessarily hard problem, we don’t need to do this

we call the resulting algorithm, together with the probabilistic cost function we describe below —— RankNet

Previous Work

RankProp

(Caruana et al., 1996)

• adv:
  • point-wise —— O(m) time complexity
• dis:
  • it is not known under what conditions it converges
  • it does not give a probabilistic model

PRank

(Herbrich et al., 2000)

• adv:
  • point-wise —— O(m) time complexity
• dis:
  • outperform by another version

“general framework”

(Dekel et al., 2004)

• dis:
  • no probabilistic model

RankBoost

(Freund et al., 2003)

similar with this paper but use decision stumps as the weak learners

A Probabilistic Ranking Cost Function

We consider models $f : R^d → R$ such that the rank order of a set of test samples is specified by the real values that f takes

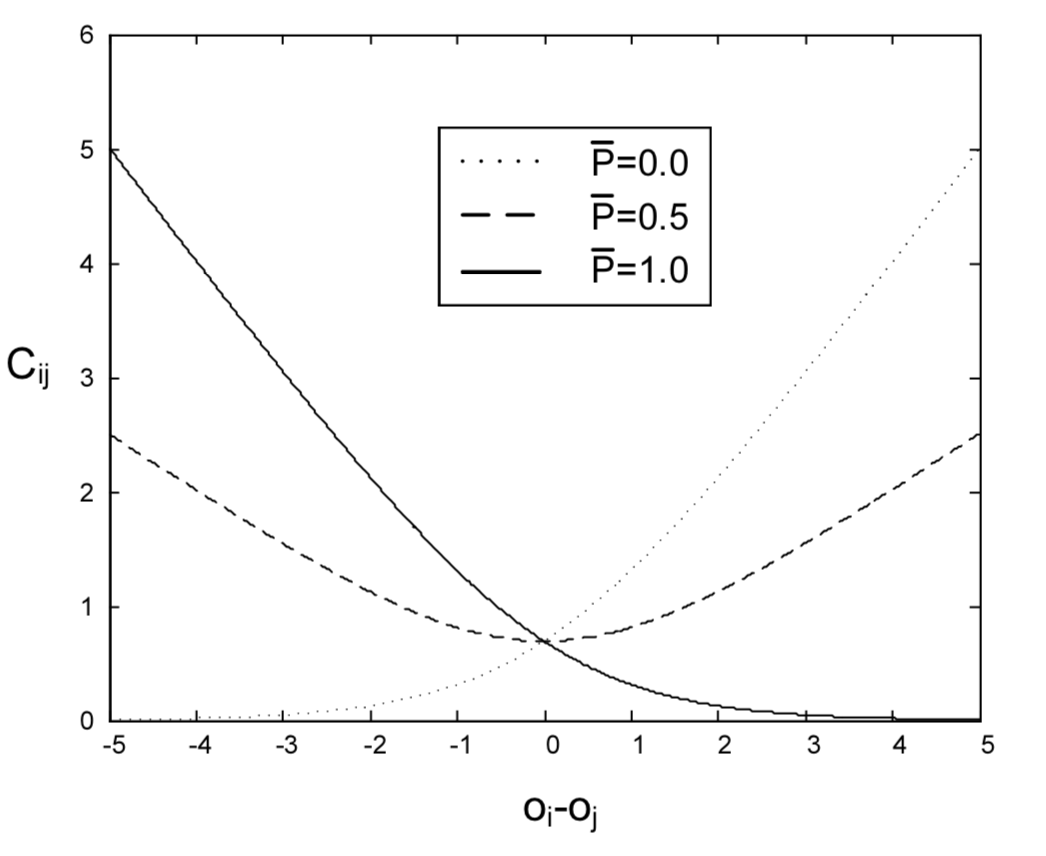
Denote the modeled posterior $P(x_i > x_j)$ by $P_{ij}$:

$$P_{ij} = \frac {e^{o_{ij}}} {1 + e^{o_{ij}}}$$

which $o_{ij} = f(x_i) - f(x_j)$

and use cross entropy cost function:

$$C_{ij} = - \bar {P}_{ij}log(P_{ij}) - (1 - \bar{P}_{ij})log(1 - P_{ij})$$

for problems with noisy labels this is likely to be more robust than a quadratic cost

Combining Probabilities

If we have $\bar P_{ij}, \bar P_{jk}$ then we have:

$$\bar P_{ik} = \frac {\bar P_{ij} \bar P_{jk}} {1 + 2\bar P_{ij} \bar P_{jk} - \bar P_{ij} - \bar P_{jk}}$$

RankNet: Learning to Rank with Neural Nets

Prove RankNet with Neural Nets is different differentiable

skip prove detail

Experiments on Artificial Data

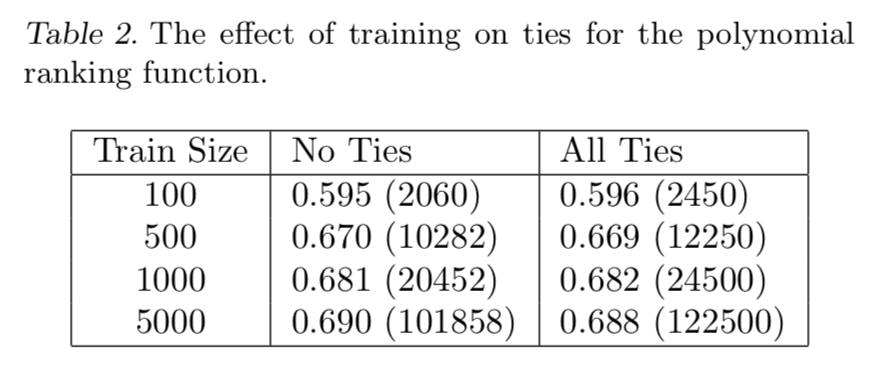
Whether there are ties in training data, results are very close

Experiments on Real Data

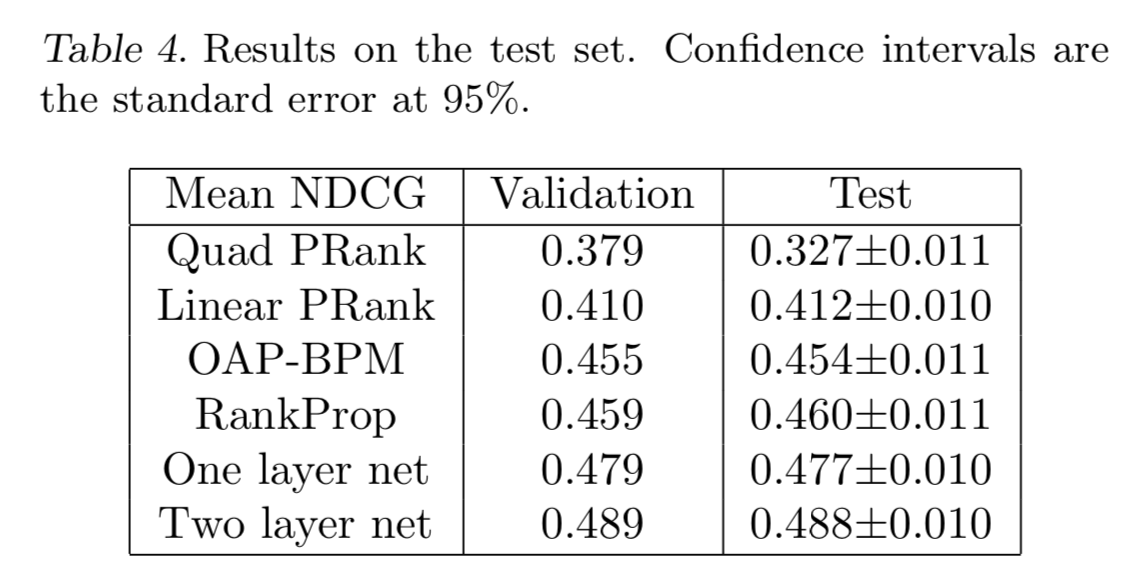
Ranking accuracy was computed using a normalized discounted cumulative gain measure（NDCG）:

$$NDCG_i \equiv N_i \sum_{j =1}^{15}(2^{r(j)} - 1) / log(1 + j)$$

where $N_i$ is a normalization constant so that a perfect ordering gets NDCG score 1
$r(j)$ is the rating of the j’th document

Discussion

Can these ideas be extended to the kernel learning framework?

depending on the kernel, the objective function may not be convex

Conclusions

skip