Berwyn's Blog
0%

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Posted on Edited on In

总结

  • 提出问题：在神经网络的训练过程中，后面层的输入是前面网络的输出，所以在前面网络参数变动的时候，后面层的输入分布一直在变化，我们称这种现象为——内部协变量漂移。这种现象会干扰神经网络训练
  • 本文提出的BN结构就是希望解决此问题，从而加速网络训练，提升训练稳定性

演变过程

  • 传统稳定分布的方式是白化——去除特征之间的相关性然后把分布变为均值为0，方差为1的高斯分布
  • 但是这种方式计算量过大且不能处处可导，所以做了两个简化
    • 把每个特征分别做处理
    • 使用mini-batch代替全体训练样本做处理
  • 计算量大大降低之后，为了保持增加模型的拟合能力，我们引进了两个可学习参数$\gamma$和$\beta$使用公式$y^{(k)} = \gamma^{(k)}\hat x^{(k)} + \beta^{(k)}$来做变换
  • 当$\gamma$等于方差且$\beta$等于均值时，等同于还原成原分布

Inference

  • 既然变换公式需要用到训练batch的mean和var，那么当模型inference的时候怎么办?
  • 文章给出的答案是在训练过程中用滑动平均的方式维护一个全局的mean和var，inference的时候就用这个代替batch的数据

应用在卷积网络

  • BN可以应用在各种网络上
  • 当应用在卷积网络上时我们把一个feature map上的所有数据当做一个特征，共享一组$\gamma$和$\beta$

优势

  • 可选用更高的初始学习率
  • 降低对于权重初始化方法的依赖
  • BN同时可作为正则化项使用从而减小/取消dropout和L2系数;
  • 提高模型训练速度
  • 在实验中达到了更高的分类精度

实验结果

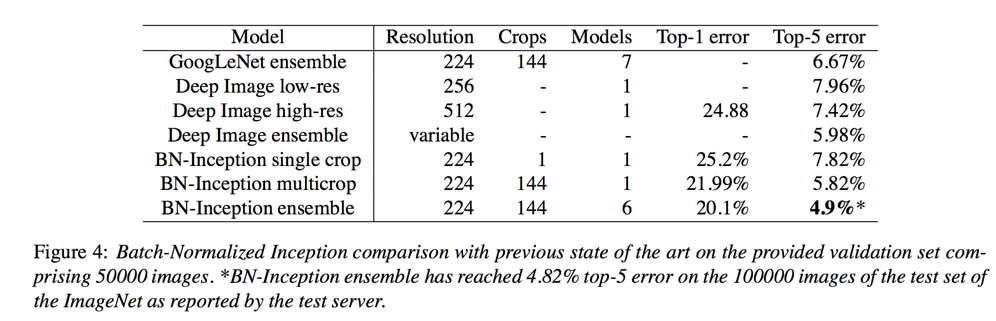
LSVRC 2012 数据集

  • ensemble(6 models, 144 crops); top5 error: 4.94%

Abstract

Training Deep Neural Networks is complicated by the fact that the distribution of each layer’s inputs changes during training

We refer to this phenomenon as internal covariate shift

Our method draws its strength from making normalization a part of the model architecture and performing the normalization for each training mini-batch

usage:

  • use much higher learning rates
  • be less careful about initialization
  • act as a regularizer
  • speed up training

Introduction

advantages in using mini-batches of example:

  • the gradient of the loss over a mini-batch is an estimate of the gradient over the training set, whose quality improves as the batch size increases
  • Second, computation over a batch can be much more efficient than m computations for individual examples, due to the parallelism afforded by the modern computing platforms

usage of Batch Normalization:

  • dramatically accelerates the training of deep neural nets
  • use much higher learning rates without the risk of divergence
  • regularizes the model and reduces the need for Dropout
  • makes it possible to use saturating nonlinearities

Towards Reducing Internal Covariate Shift

Internal Covariate Shift——change in the distribution of network activations due to the change in network parameters during training

target:

  • To improve the training, we seek to reduce the internal covariate shift

how:

  • fixing the distribution of the layer inputs x as the training progresses
  • the network training converges faster if its inputs are whitened
  • however, whitening the layer inputs is expensive and not everywhere differentiable
  • we want to find another way

Normalization via Mini-Batch Statistics

Since the full whitening of each layer’s inputs is costly and not everywhere differentiable we make two necessary simplifications:

  • instead of whitening the features in layer inputs and outputs jointly, we will normalize each scalar feature independently
  • we introduce, for each activation $x^{(k)}$, a pair of parameters $\gamma^{(k)}, \beta^{(k)}$, which scale and shift the normalized value:
  • since we use mini-batches in stochastic gradient training, each mini-batch produces estimates of the mean and variance of each activation

BN transform as follow:

Alt text

Training and Inference with Batch-Normalized Networks

  • BN is neither necessary nor desirable during inference
  • using moving averages to calculate means and variances using during inference

Batch-Normalized Convolutional Networks

  • the bias b can be ignored
  • $z = g(Wu + b)$ is replaced with $z = g(BN(Wu))$
  • we use the effective mini-batch of size $m’ = |B| = m p q$ where $p, q$ is the width and height of feature map
  • i.e. we learn a pair of parameters $\gamma^{(k)}$ and $\beta^{(k)}$ per feature map, rather than per activation

Batch Normalization enables higher learning rates

  • it prevents small changes to the parameters from amplifying into larger and suboptimal changes in activations in gradients
  • BN also makes training more resilient to the parameter scale

Batch Normalization regularizes the model

  • a training example is seen in conjunction with other examples in the mini-batch
  • the training network no longer producing deterministic values for a given training example

Experiments

Activations over time

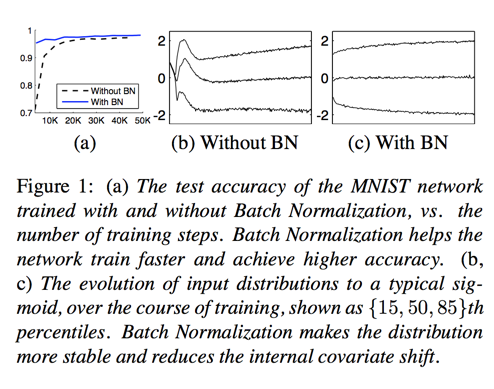
Alt text

ImageNet Classification

network is Inception except the 5 × 5 convolutional layers are replaced by two consecutive layers of 3 × 3 convolutions with up to 128 filters.

Accelerating BN Networks

further changed the network and its training parameters as follows:

  • increase learning rate
  • remove dropout
  • reduce the $L_2$ weight regularzation by a factor of 5
  • accelerate the learning rate decay —— 6 times faster
  • Remove Local Response Normalization
  • Shuffle training examples more thoroughly
  • Reduce the photometric distortions

Single-Network Classification

evaluated network list:

  • Inception
  • BN-Baseline: Same as Inception with Batch Normalization before each nonlinearity
  • BN-x5: The initial learning rate was increased by a factor of 5, to 0.0075
  • BN-x30: Like BN-x5, but with initial learning rate 0.045
  • BN-x5-Sigmoid: Like BN-x5, but with sigmoid nonlinearity instead ReLU

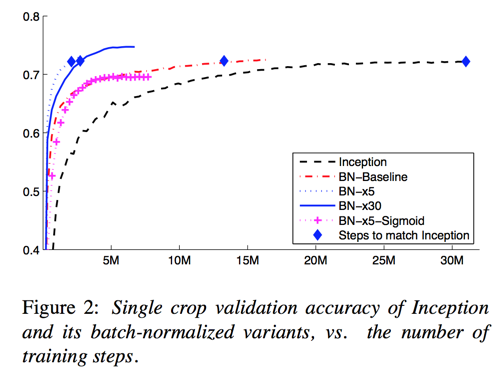
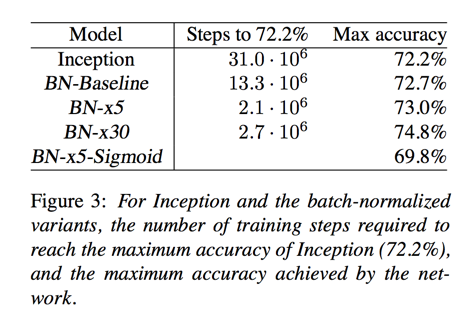
Alt text

Alt text

Ensemble Classification

Alt text

Conclusion

skip